Abstract
In this work, the absorption coefficient of a metallic photonic crystal doped with nanoparticles has been obtained using numerical simulation techniques. The effects of quantum interference and the concentration of doped particles on the absorption coefficient of the system have been investigated. The nanoparticles have been considered as semiconductor quantum dots which behave as a four-level quantum system and are driven by a single coherent laser field. The results show that changing the position of the photonic band gap about the resonant energy of the two lower levels directly affects the decay rate, and the system can be switched between transparent and opaque states if the probe laser field is tuned to the resonance frequency. These results provide an application for metallic nanostructures in the fabrication of new optical switches and photonic devices.
Similar content being viewed by others
Introduction
In the past few decades, there has been a growing interest in the development of artificial nano-materials. One class of material such as this is photonic crystals (PCs), which are periodic dielectric or semiconductor structures that display a photonic band gap (PBG) in their electromagnetic wave transmission characteristics [1–4]. The existence of the PBG has inspired the design of various nano-optical and opto-electronic devices [5]. Since the formation of the PBG is due to the multiple Bragg reflections within a PC, ordinary PCs are a combination of lossless materials for which the stop band has a small width, almost less than 25% of the central frequency. This is due to the fact that a significant percentage of incident radiation passes through the periodic structure cores so that the reflected radiation is weaker than the transmitted radiation. Because of this, Bragg scattering comes into play when there are periodicities along the direction of propagation. To exhibit a noticeable PBG with fewer periodicities it is much better to use impenetrable materials. Metals would be one of the best options since they are more reflective than dielectric or semiconductor materials over a broad range of frequencies, due to their imaginary dielectric component that exists in even the optical and near infrared regions, where metals are dispersive and absorptive in these frequency regions [6–8]. Recently, considerable progress has been made in constructing these periodic arrangements which are called metallic or metallodielectric photonic crystals (MPC/MDPC) in one-, two-, and three-dimensional systems. For instance, one-dimensional (1D) MDPCs with metal thicknesses on the order of hundreds of nanometres has been proved transparent to visible light while blocking ultraviolet and infrared [9, 10]. This characteristic can be used for example in laser safety glasses, UV protective films and flat panel displays. Two-dimensional (2D) MPC structures are usually made of metallic rods or nanodisks that are periodically arranged on a waveguide layer. Waveguided MPCs have exhibited unique optical properties because of the strong coupling that exists between the particle plasmon resonance and waveguide mode. Such structures have a number of potential applications in biosensors [11] and all-optical switching [12], among others. In the case of three-dimensional (3D) structures, there are also several applications such as high-efficiency light sources [13] and thermal photovoltaic power generation [14].
Besides these advantages, PCs can be used for radiation suppression and emission enhancement below the electronic band gap and near a photonic band edge, respectively, where a PC functions as a reservoir for an exited light emitter or active medium such as an atom, a molecule or a quantum dot (QD). According to Fermi’s ‘Golden Rule’, the decay rate is proportional to the local density of states (LDOS) that counts the number of electromagnetic modes available to the photons for emission into the environment. Thus, any modification in the LDOS would lead to manipulation of the decay rate. Recently, the inhibition, enhancement and quantum interference (QI) effects of spontaneous emission (SE) from the QDs doped in 3D–PCs have been widely studied, both experimentally and theoretically [15–19]. Controlling spontaneous emission by using quantum optics would lead to several interesting effects, such as optical gain enhancement [20] and photoluminescence enhancement [21], optical switching [22, 23], quantum information processing [24, 25] and electromagnetically induced transparency [26]. QI in a three- or multi-level atomic system can arise from the superposition of SEs when electron transitions take place between the upper and lower levels. Under certain circumstances the initially excited atomic system may not decay to its ground level due to a cancellation of SE by QI between atomic transition levels. Due to this, dark states with zero absorption amplitude would appear causing the multi-level atomic system to act like a transparent medium, which has potential applications for optical switches and photonic devices [27, 28]. In this paper, the effects of electronic QI on the absorption coefficient of QDs have been investigated for small and large concentration of the dopants (QDs). We consider that the QDs are four–energy level systems where the two upper levels are very close, coupled to a lower one via the same and single field continuum and damped by the MPC interaction.
Metallic Photonic Crystals
Recently, theoretical and experimental studies have shown that it is possible to make 3D MPCs that contain nano-sized metallic spheres which are transparent to visible and near infrared light [7, 29, 30]. In this paper, we have used an ideal 3D isotropic MPC model made from metallic spheres of radius a with a frequency dependent refractive index n1(ω), which are arranged periodically in a background dielectric material with a constant refractive index (n2). The dispersion relation and photonic band structure of this idealized theoretical 3D model was developed by S. John in the following references [31, 32]. Although many simplifying approximations have been used in this model, it is sufficient for our purpose as it leads to qualitatively correct physics and exhibits many of the observed and computed characteristics of 3D MPC which opens a band gap in the rage of visible frequencies [7, 29, 30].
In many photonic band structure calculations related to MPCs, the refractive index function for metallic materials is derived using the Drude model [33, 34], which offers an excellent fit to measured data over a wide frequency range. Using this model, the refractive index for a metallic material is expressed as

where ω ωp and γ are the frequency of the incident laser beam, the plasma frequency and the damping factor of the conduction-band electrons, respectively. The plasma frequency is defined by  , where N0 is the electron density, meff is the effective mass of the electron, e is the electron charge and ε0 is the permittivity of the free space. The damping rate (which is also called the electron collision rate) is the inverse of the mean electron collision time. The parameter γ is frequency independent and therefore absorption can be neglected at optical frequencies, since γ/ω = 1. As one can see from Eq. (1), for frequencies below ωp, the local wave vector is imaginary and the metal behaves as a dispersive and absorptive environment. Nonetheless, if the diameter of the metallic spheres in our crystal structures can be chosen close to or smaller than the relevant skin depth of the corresponding metal, the EM wave can be transmitted by tunnelling through the structure. The position of the PBG can be determined by selection of proper thicknesses and refractive indices. Since we are interested in optical frequencies, the radius of the metallic spheres and lattice constant of the PC have been chosen in reduced units as a = 0.25ħc/ε
p
and L = 10.5ħc/ε
p
, respectively. In these parameters, ħ is the reduced Planck constant and ε
p
is the plasmon energy, i.e. ε
p
= ħωp. A plot of the band structure of the PC consisting of spherical metal nanoparticles in a dielectric background (n2 = 1.5) has been illustrated in Fig. 1.
, where N0 is the electron density, meff is the effective mass of the electron, e is the electron charge and ε0 is the permittivity of the free space. The damping rate (which is also called the electron collision rate) is the inverse of the mean electron collision time. The parameter γ is frequency independent and therefore absorption can be neglected at optical frequencies, since γ/ω = 1. As one can see from Eq. (1), for frequencies below ωp, the local wave vector is imaginary and the metal behaves as a dispersive and absorptive environment. Nonetheless, if the diameter of the metallic spheres in our crystal structures can be chosen close to or smaller than the relevant skin depth of the corresponding metal, the EM wave can be transmitted by tunnelling through the structure. The position of the PBG can be determined by selection of proper thicknesses and refractive indices. Since we are interested in optical frequencies, the radius of the metallic spheres and lattice constant of the PC have been chosen in reduced units as a = 0.25ħc/ε
p
and L = 10.5ħc/ε
p
, respectively. In these parameters, ħ is the reduced Planck constant and ε
p
is the plasmon energy, i.e. ε
p
= ħωp. A plot of the band structure of the PC consisting of spherical metal nanoparticles in a dielectric background (n2 = 1.5) has been illustrated in Fig. 1.
Plot of the Bloch wave vector K as a function of the normalized photon energy for a metallic PBG. The vertical dashed lines show ε v /ε p and ε c /ε p which are the maximum normalized energy of the lower energy band and the minimum normalized energy of the upper energy band, respectively. The refractive index of background is n2 = 1.5
Active Medium Embedded in a MPC
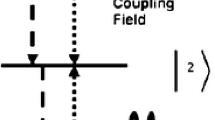
The nano-sized active medium in the 3D MPC considered here is assumed to be four-level QDs, with diameters ranging from 2 to 10 nanometres, and two upper levels |c〉 and |b〉 which are close to one another. The remaining two lower levels are denoted as |a〉 and |d〉. The two upper levels are dipole coupled to the |a〉 state via the same single field continuum. We also assume that SE is allowed from the excited states (upper levels) to the |a〉 state and from |a〉 state to |d〉 state, whereas the transition |b〉 → |d〉, |c〉 → |d〉 and |c〉 → |b〉 are inhibited in the electric dipole approximation. There are many potential QDs suitable for our theoretical model such as CdSe/ZnS [17] or InAs/GaAs [35] core–shell QDs. The energy level schematic is shown in Fig. 2.
Four-level QD with the two upper levels |c〉 and |b〉 which are near one another, and two lower levels |a〉 and |d〉. Here, ω is the probe field frequency while ωca and ωba are the transition frequencies.Γc and Γb are the decay rates from the exited states to the |a〉 state. The decay rate from |a〉 to |d〉 is given as Γa, whereas Δc = ωca − ω and Δ b = ω − ωba are the detunings of the atomic transition energies.δ k is the detuning of the probe field, which has a central frequency at the middle point of the two upper levels
System Hamiltonian and Density Matrix Equations
In this section, the interaction between QDs doped within the PBG reservoir and a probe field with slowly varying amplitude is investigated. The total semiclassical Hamiltonian of the system can be written as

Here, HQ, HQF, HR, HQR and HQQ are the Hamiltonians of the four-level QD, the QD–field interaction, the PBG reservoir, the QD–PBG reservoir interaction and QDs–QDs interaction, respectively [36, 37].
Using Eq. (2), the equation of motion of the density matrix elements can be written as follows [38]:






where

In Eqs. (3-9), ρ ij (i j = a, b, c or d) are density matrix elements (coherences), p is the strength of quantum interference and is defined by p = μac·μab/μacμab. In this paper, the maximum quantum interface has been considered, which corresponds to a dipole transition moment μac that is parallel to μab. This gives p = 1. Here, μac and μab are the electric dipole moments induced by the transitions |a〉 ↔ |b〉 and |a〉 ↔ |c〉, respectively. Since the two upper energy levels are very close (εbc = 0.03 eV), it is reasonable to consider μab = μab = μ. Ω is the Rabi frequency of the probe field, defined as Ω = μE/2ħ, where the dipolar transition moments and external field E are parallel. The parameters α and β are related to the interaction of QDs when the MPC is densely doped [37]. This interaction is called dipole–dipole interaction (DDI), and its effect was calculated using mean-field theory. The dependency of all decay rates to energy and local density of states can be written as

Here, the function Z(ε) is called the form factor, which contains the information about the electron–photon interaction and is obtained in reference [39–41].
For simplicity, all parameters have been normalized with respect to (ΓbΓc)1/2/2, which gives a constant value for the resonant energies εab and εac. Here, γ0 is the decay rate (line-width) for an excited electron in a QD when it is located in a vacuum. The expression of the absorption coefficient is written in terms of density matrix coherence as [37]:

where

Here, N is the concentration of quantum dots and ε is the energy of the incident laser beam.
Numerical Simulation
In order to study the linear response of the system, we have calculated the normalized absorption coefficient given in Eq. (11) (α/α0) by using a very low driving field (Ω = 0.01). We consider that the metallic spheres are made of silver with ε p = 9 eV. The two upper resonant energies (εab = 2.78 eV and εac= 2.783 eV) are considered to be far away from the upper edge band gap in the first Brillouin zone where Γb ≈ Γc= 1.57γ0. The value of Γa can be set by changing the resonant energy εad. This decay rate (Γa) can be totally suppressed if the resonant energy lies within the band gap.
The system of equations in (3–8) has been solved numerically for cases where DDI was neglected and taken into account while the system approaches a steady state configuration. The results have been shown in Figs. 3 and 4 where the normalized absorption coefficient versus the detuning parameter has been drawn for different values of lower decay rate (Γa = 0.000, 0.005 and 0.100). As one can see, in both cases, increasing Γa causes the system to switch between transparent and opaque states. This means that when the lower resonance state (i.e. |a〉-|d〉) lies within the band gap, the normalized absorption coefficient is zero, and when it goes further from the band gap it is nonzero. This behaviour demonstrates the switching between absorption and nonabsorption states that can be used to make optical switches.
Conclusions
In conclusion, we have studied the effect the quantum interference and DDI on the absorption of a MPC doped with an ensemble of four-level QDs, for both cases where DDI was neglected or accounted for, while the system approached a steady state. A single driving laser field which induces a dipole moment in each QD was applied to measure the absorption. The density matrix method and linear-response theory have been used to calculate the absorption.
It is found that when the resonance energy of the lower levels is within the band gap, the system is in an absorbing state. However, when the resonance energy of the lower levels is outside the band gap, the system is in a nonabsorption state. Thus, the system can be switched between the absorption and nonabsorption states. We anticipate that the results described here will be useful for developing new types of optical switching devices.
References
Yablonovitch E: Phys. Rev. Lett.. 1987, 58: 2059. COI number [1:CAS:528:DyaL2sXktFGit7Y%3D]; Bibcode number [1987PhRvL..58.2059Y] COI number [1:CAS:528:DyaL2sXktFGit7Y%3D]; Bibcode number [1987PhRvL..58.2059Y] 10.1103/PhysRevLett.58.2059
John S: Phys. Rev. Lett.. 1987, 58: 2486. COI number [1:CAS:528:DyaL2sXks1KksL0%3D]; Bibcode number [1987PhRvL..58.2486J] COI number [1:CAS:528:DyaL2sXks1KksL0%3D]; Bibcode number [1987PhRvL..58.2486J] 10.1103/PhysRevLett.58.2486
John SGJ, Joannopoulos D, Winn JN, Meade RD: Photonic Crystals: Molding the Flow of Light. Princeton University Press, Princeton; 1995.
Soukoulis CM: Photonic Crystals and Light Localization in the 21st Century. Springer, New York; 2001.
Yasumoto K: Electromagnetic Theory and Applications for Photonic Crystals. CRC Press, Boca Raton, FL; 2006.
Brown ER, McMahon OB: Appl. Phys.Lett.. 1995, 67: 2138. COI number [1:CAS:528:DyaK2MXos1SgsLs%3D]; Bibcode number [1995ApPhL..67.2138B] COI number [1:CAS:528:DyaK2MXos1SgsLs%3D]; Bibcode number [1995ApPhL..67.2138B] 10.1063/1.114745
Wang Z, Chan CT, Zhang W, Ming N, Sheng P: Phys. Rev. B Condens Matter Mat. Phy.. 2001, 64: 1131081.
Fleming JG, Lin SY, El-Kady I, Biswas R, Ho KM: Nature. 2002, 417: 52. COI number [1:CAS:528:DC%2BD38XjsFOgtb4%3D]; Bibcode number [2002Natur.417...52F] COI number [1:CAS:528:DC%2BD38XjsFOgtb4%3D]; Bibcode number [2002Natur.417...52F] 10.1038/417052a
Scalora M, Bloemer MJ, Pethel AS, Dowling JP, Bowden CM, Manka AS: J. Appl. Phys.. 1998, 83: 2377. COI number [1:CAS:528:DyaK1cXhtFOku78%3D]; Bibcode number [1998JAP....83.2377S] COI number [1:CAS:528:DyaK1cXhtFOku78%3D]; Bibcode number [1998JAP....83.2377S] 10.1063/1.366996
Bloemer MJ, Scalora M: Appl. Phys. Lett.. 1998, 72: 1676. COI number [1:CAS:528:DyaK1cXitVWntb8%3D]; Bibcode number [1998ApPhL..72.1676B] COI number [1:CAS:528:DyaK1cXitVWntb8%3D]; Bibcode number [1998ApPhL..72.1676B] 10.1063/1.121150
Raschke G, Kowarik S, Franzl T, Sonnichsen C, Klar TA, Feldmann J, Nichtl A, Kurzinger K: Nano Lett.. 2003, 3: 935. COI number [1:CAS:528:DC%2BD3sXktFSqsLg%3D]; Bibcode number [2003NanoL...3..935R] COI number [1:CAS:528:DC%2BD3sXktFSqsLg%3D]; Bibcode number [2003NanoL...3..935R] 10.1021/nl034223+
Cuesta-Soto F, MartiÌnez A, GarciÌa J, Ramos F, Sanchis P, Blasco J, MartiÌ J: Opt. Express. 2004, 12: 161. COI number [1:STN:280:DC%2BD1Mznt1aktg%3D%3D]; Bibcode number [2004OExpr..12..161C] COI number [1:STN:280:DC%2BD1Mznt1aktg%3D%3D]; Bibcode number [2004OExpr..12..161C] 10.1364/OPEX.12.000161
Puscasu I, Pralle M, McNeal M, Daly J, Greenwald A, Johnson E, Biswas R, Ding CG: J. Appl. Phys.. 2005, 98: 1. 10.1063/1.1947899
Lin SY, Fleming JG, El-Kady I: Opt. Lett.. 2003, 28: 1683. COI number [1:CAS:528:DC%2BD3sXnvVSgtLc%3D]; Bibcode number [2003OptL...28.1683L] COI number [1:CAS:528:DC%2BD3sXnvVSgtLc%3D]; Bibcode number [2003OptL...28.1683L] 10.1364/OL.28.001683
Lodahl P, Van Driel AF, Nikolaev IS, Irman A, Overgaag K, Vanmaekelbergh D, Vos WL: Nature. 2004, 430: 654. COI number [1:CAS:528:DC%2BD2cXmt1GisLk%3D]; Bibcode number [2004Natur.430..654L] COI number [1:CAS:528:DC%2BD2cXmt1GisLk%3D]; Bibcode number [2004Natur.430..654L] 10.1038/nature02772
Paspalakis E, Kylstra NJ, Knight PL: Phys. Rev. A. 1999, 60: R33. COI number [1:CAS:528:DyaK1MXktVSnsr8%3D]; Bibcode number [1999PhRvA..60...33P] COI number [1:CAS:528:DyaK1MXktVSnsr8%3D]; Bibcode number [1999PhRvA..60...33P] 10.1103/PhysRevA.60.R33
John S, Busch K: J. Lightwave Technol.. 1999, 17: 1931. COI number [1:CAS:528:DyaK1MXotVOmu7c%3D]; Bibcode number [1999JLwT...17.1931J] COI number [1:CAS:528:DyaK1MXotVOmu7c%3D]; Bibcode number [1999JLwT...17.1931J] 10.1109/50.802976
John S, Quang T: Phys. Rev. A. 1994, 50: 1764. COI number [1:CAS:528:DyaK2cXls1Khtb4%3D]; Bibcode number [1994PhRvA..50.1764J] COI number [1:CAS:528:DyaK2cXls1Khtb4%3D]; Bibcode number [1994PhRvA..50.1764J] 10.1103/PhysRevA.50.1764
Zhu SY, Chen H, Huang H: Phys. Rev. Lett.. 1997, 79: 205. COI number [1:CAS:528:DyaK2sXks1Ghsbo%3D]; Bibcode number [1997PhRvL..79..205Z] COI number [1:CAS:528:DyaK2sXks1Ghsbo%3D]; Bibcode number [1997PhRvL..79..205Z] 10.1103/PhysRevLett.79.205
Vlasov YA, Luterova K, Pelant I, HoÌ̂nerlage B, Astratov VN: Thin Solid Films. 1998, 318: 93. COI number [1:CAS:528:DyaK1cXis1agsLk%3D]; Bibcode number [1998TSF...318...93V] COI number [1:CAS:528:DyaK1cXis1agsLk%3D]; Bibcode number [1998TSF...318...93V] 10.1016/S0040-6090(97)01146-2
Liu K, Tsu R: Microelectronics J.. 2009, 40: 741. COI number [1:CAS:528:DC%2BD1MXksVOhtr0%3D] COI number [1:CAS:528:DC%2BD1MXksVOhtr0%3D] 10.1016/j.mejo.2008.11.052
Asakawa K, Sugimoto Y, Watanabe Y, Ozaki N, Mizutani A, Takata Y, Kitagawa Y, Ishikawa H, Ikeda N, Awazu K, Wang X, Watanabe A, Nakamura S, Ohkouchi S, Inoue K, Kristensen M, Sigmund O, Borel PI, Baets R: New J. Phys.. 2006, 8: 208. Bibcode number [2006NJPh....8..208A] Bibcode number [2006NJPh....8..208A] 10.1088/1367-2630/8/9/208
Nakamura H, Sugimoto Y, Kanamoto K, Ikeda N, Tanaka Y, Nakamura Y, Ohkouchi S, Watanabe Y, Inoue K, Ishikawa H, Asakawa K: Opt. Express. 2004, 12: 6606. Bibcode number [2004OExpr..12.6606N] Bibcode number [2004OExpr..12.6606N] 10.1364/OPEX.12.006606
Yoshle T, Scherer A, Hendrickson J, Khitrova G, Gibbs HM, Rupper G, Ell C, Shchekin OB, Deppe DG: Nature. 2004, 432: 200. Bibcode number [2004Natur.432..200Y] Bibcode number [2004Natur.432..200Y] 10.1038/nature03119
Hennessy K, Badolato A, Winger M, Gerace D, Atature M, Gulde S, Falt S, Hu EL, Imamoglu A: Nature. 2007, 445: 896. COI number [1:CAS:528:DC%2BD2sXhvFGitbk%3D]; Bibcode number [2007Natur.445..896H] COI number [1:CAS:528:DC%2BD2sXhvFGitbk%3D]; Bibcode number [2007Natur.445..896H] 10.1038/nature05586
Singh MR: Phys. Rev. A At. Mol. Opt. Phys.. 2004, 70: 033813. Bibcode number [2004PhRvA..70C3813S] Bibcode number [2004PhRvA..70C3813S]
Akram U, Ficek Z, Swain S: J. Mod. Opt.. 2001, 48: 1059. COI number [1:CAS:528:DC%2BD3MXkt1Oiu7c%3D]; Bibcode number [2001JMOp...48.1059A] COI number [1:CAS:528:DC%2BD3MXkt1Oiu7c%3D]; Bibcode number [2001JMOp...48.1059A]
Zhou P, Swain S: Phys. Rev. A At. Mol. Opt. Phys.. 1997, 56: 3011. COI number [1:CAS:528:DyaK2sXmsFOmurw%3D]; Bibcode number [1997PhRvA..56.3011Z] COI number [1:CAS:528:DyaK2sXmsFOmurw%3D]; Bibcode number [1997PhRvA..56.3011Z]
Eradat N, Huang JD, Vardeny ZV, Zakhidov AA, Khayrullin I, Udod I, Baughman RH: Synth. Met.. 2001, 116: 501. COI number [1:CAS:528:DC%2BD3cXovFOks70%3D] COI number [1:CAS:528:DC%2BD3cXovFOks70%3D] 10.1016/S0379-6779(00)00423-9
El-Kady I, Sigalas MM, Biswas R, Ho KM, Soukoulis CM: Phys. Rev. B Condens. Matter. Mat. Phys.. 2000, 62: 15299. COI number [1:CAS:528:DC%2BD3cXovVKhu7w%3D]; Bibcode number [2000PhRvB..6215299E] COI number [1:CAS:528:DC%2BD3cXovVKhu7w%3D]; Bibcode number [2000PhRvB..6215299E] 10.1103/PhysRevB.62.15299
John S, Wang J: Phys. Rev. Lett.. 1990, 64: 2418. COI number [1:CAS:528:DyaK3cXksVylu7o%3D]; Bibcode number [1990PhRvL..64.2418J] COI number [1:CAS:528:DyaK3cXksVylu7o%3D]; Bibcode number [1990PhRvL..64.2418J] 10.1103/PhysRevLett.64.2418
John S, Wang J: Phys. Rev. B. 1991, 43: 12772. Bibcode number [1991PhRvB..4312772J] Bibcode number [1991PhRvB..4312772J] 10.1103/PhysRevB.43.12772
Lourtioz JM: Photonic Crystals: Towards Nanoscale Photonic Devices. Springer, New York; 2005.
Singh MR: Phys. Rev. A. 2009, 79: 013826–1. Bibcode number [2009PhRvA..79a3826S] Bibcode number [2009PhRvA..79a3826S]
Gerardot BD, Brunner D, Dalgarno PA, Karrai K, Badolato A, Petroff PM, Warburton RJ: New J. Phys.. 2009, 11: 013028. Bibcode number [2009NJPh...11a3028G] Bibcode number [2009NJPh...11a3028G] 10.1088/1367-2630/11/1/013028
Haque I, Singh MR: J. Phys.: Condens. Matter. 2007, 19: 156229. Bibcode number [2007JPCM...19o6229H] Bibcode number [2007JPCM...19o6229H] 10.1088/0953-8984/19/15/156229
Singh MR: Phys. Rev. A. 2007, 75: 043809. Bibcode number [2007PhRvA..75d3809S] Bibcode number [2007PhRvA..75d3809S] 10.1103/PhysRevA.75.043809
Marlan Orvil Scully MSZ: Quantum Optics. Cambridge University Press, Cambridge; 1997.
Rupasov VI, Singh M: Phys. Rev. Lett.. 1996, 77: 338. COI number [1:CAS:528:DyaK28XktVahsLs%3D]; Bibcode number [1996PhRvL..77..338R] COI number [1:CAS:528:DyaK28XktVahsLs%3D]; Bibcode number [1996PhRvL..77..338R] 10.1103/PhysRevLett.77.338
Rupasov VI, Singh M: Phys. Rev. A At. Mol. Opt. Phys.. 1996, 54: 3614. COI number [1:CAS:528:DyaK28Xmtlaksr8%3D]; Bibcode number [1996PhRvA..54.3614R] COI number [1:CAS:528:DyaK28Xmtlaksr8%3D]; Bibcode number [1996PhRvA..54.3614R]
Rupasov VI, Singh M: Phys. Rev. A At. Mol. Opt. Phys.. 1997, 56: 898. COI number [1:CAS:528:DyaK2sXksFSmtrY%3D]; Bibcode number [1997PhRvA..56..898R] COI number [1:CAS:528:DyaK2sXksFSmtrY%3D]; Bibcode number [1997PhRvA..56..898R]
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hatef, A., Singh, M. The Study of Quantum Interference in Metallic Photonic Crystals Doped with Four-Level Quantum Dots. Nanoscale Res Lett 5, 464 (2010). https://doi.org/10.1007/s11671-009-9517-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11671-009-9517-1