Abstract
Nanoindentation processes in single crystal Ag thin film under different crystallographic orientations and various indenter widths are simulated by the quasicontinuum method. The nanoindentation deformation processes under influences of crystalline anisotropy and indenter size are investigated about hardness, load distribution, critical load for first dislocation emission and strain energy under the indenter. The simulation results are compared with previous experimental results and Rice-Thomson (R-T) dislocation model solution. It is shown that entirely different dislocation activities are presented under the effect of crystalline anisotropy during nanoindentation. The sharp load drops in the load–displacement curves are caused by the different dislocation activities. Both crystalline anisotropy and indenter size are found to have distinct effect on hardness, contact stress distribution, critical load for first dislocation emission and strain energy under the indenter. The above quantities are decreased at the indenter into Ag thin film along the crystal orientation with more favorable slip directions that easy trigger slip systems; whereas those will increase at the indenter into Ag thin film along the crystal orientation with less or without favorable slip directions that hard trigger slip systems. The results are shown to be in good agreement with experimental results and R-T dislocation model solution.
Introduction
Nanostructural materials have been the subject of intensive research in recent years due to its unique mechanical properties [1, 2]. Research has shown that these unique mechanical properties are closely related to internal structure of nanomaterials and deformation mechanism [3]. Nanoindentation is a complicated contact problem [4–6], which has become a standard technique for evaluating the mechanical properties of thin film. During nanoindentation, it can be strongly influenced by crystalline anisotropy [7, 8] and indentation size effect (ISE) [9, 10], besides test equipment, surface roughness [11, 12], substrate effects [13], grain boundaries effects [14], pre-existing defects [15, 16] and indenter geometry [17, 18]. Groenou et al. [19] investigated slip patterns on a single crystal MnZn ferrite workpiece by spherical indentation on (100), (011) and (111) crystallographic planes. Khan et al. [20] studied the deformation behavior and hardness in indentation of a single crystal MgO using Vickers and spherical indenter, and showed that crystal orientation has a distinct influence on the indentation crack patterns. Recently, a number of experiments [21–23] have pointed out the well-known indentation size effect for metals, in which the hardness is observed to increase with decreasing indentation size.
However, it is difficult to directly examine the dislocation activities by experiments. One of the available methods is the atomic scale simulations to identify microscopic mechanisms, and to put insights into microscopic behavior such as molecular dynamics (MD) that can effectively simulate the dynamic behavior of nanomaterials. Due to the computational intensity of the problem, many of MD simulations are limited to relatively small spatial sizes or very high loading rates, and inevitably include boundary effects. For example, Tsuru and Shibutani [24] performed the atomistic simulation of nanoindentation via MD and investigated anisotropic effect in elastic and incipient plastic behavior under nanoindentation. However, atomic model studied in this simulation is only 20 nm thick and 18 nm wide, it is hard to exclude boundary effect and especially to study size effect. Multiscale atomic simulation is in general more flexible and more efficient than fully atomic simulations when dealing with complicated dislocation configurations in relatively large atomic systems. The quasicontinuum (QC) method [25, 26] is one of the successful multiscale atomic simulations, which has been capable of implementing large-scale simulations without losing calculation precision. Nowadays, this novel method has been successfully applied to investigate the dislocation nucleation and interactions [27, 28], nanoindentation [29–32] and fracture [33]. Using the QC method, Wang et al. [34, 35] investigated the size effect of the indenter and the microscopic mechanisms of dislocation deformation during nanoindentation. Dupont and Sansoz [36] examined the mechanical behavior and underlying mechanisms of surface plasticity in nanocrystalline Al with a grain diameter of 7 nm deformed under wedge-like cylindrical contact. Recently, Jin et al. [37] studied the dislocation nucleation and interactions at the onset of plasticity for the nanoindentation of the (001) surface of a single crystal Al using the QC method. They found that the sharp load drops in the load–displacement curves are associated with deformation twinning and collective dislocation activities. However, Jin et al. [37] is not enough to deeply discuss collective dislocation activities due to the shallow indentation depth (the maximum indentation depth is only 1.6 nm).
The above discussions motivate us to understand the nature of crystalline anisotropy and indenter size on the onset of plasticity during nanoindentation without boundary effect. The QC method is employed to study the nanoindentation deformation processes under different crystalline orientation and various indenter size, respectively. The organization of the remainder of the paper is as follows: First, the choice of the nanoindentation orientations and the QC method adopted are briefly introduced in Sect. “Nanoindentation Simulation”. Subsequently, a series of different dislocation activities and underlying deformation mechanisms of nanoindentation under different crystallographic orientations on single crystal Ag thin film are analyzed in Sect. “Results and Analysis”. Then, the influences of crystalline anisotropy and indenter size on hardness, contact stress distribution, critical load for first dislocation emission and strain energy under the indenter are discussed, and the simulation results are compared with experimental results and Rice-Thomson (R-T) dislocation model solution in Sect. “Discussion”. Finally, some concluding remarks are made in Sect. “Conclusions”.
Nanoindentation Simulation
Description of the Nanoindentation Model
The QC method proposed by Tadmor et al. [25] in 1996 is a remarkably successful multiscale simulation method. This method is a molecular static technique finding the solution of equilibrium atomic configurations by energy minimization, given externally imposed forces or displacements. The problem is modeled without explicitly representing every atom in the cell; the regions of small deformation gradients are treated as a continuum media by the finite element method. The major reasons that the QC method is selected in this investigation are that: (1) It can describe larger-scale atomic systems in which <1% of the total atoms are treated explicitly [25]; (2) Compared with a single scale method, such as MD, the QC method is able to save considerable computing time while maintaining sufficient accuracy [38]; (3) The issues with artificial boundary conditions encountered in MD can be avoided [39]; (4) The automatic adaptation mesh criterion is adopted to reduce the degrees of freedom and computational demand without losing atomistic detail in regions where it is required [26]. More details on the QC method can be found in Refs. [25] and [26].
During the QC simulation, the energy of atom was calculated by the embedded atom method (EAM). The Voter potential was used for the simulation of FCC single crystal Ag thin film [40]. The material’s parameters from the EAM potential are given as follows: Lattice constant (l0) is 0.4090 nm, Burgers vector module (b) is 0.289 nm, Shear modulus (μ) is 33.81 GPa and Poisson’s ratio (ν) is 0.353. The schematic representation of nanoindentation model is displayed in Fig. 1. The thin film investigated in this simulation is 100 nm thick, 200 nm wide and infinite in the out-of-plane direction with periodic boundary conditions. The model size used in QC simulation is larger by an order of magnitude than that in MD simulation. For the purpose of simplicity, the indenter used in the present investigation is modeled as a rectangular rigid body. The width of indenters (2a) is 4d, 8d, 12d, 16d and 20d (in which,  is the spacing between the adjacent (111) planes), respectively. The effect of coefficient of friction on the nanoindentation behavior of single crystal copper has been investigated by Liu et al. [41], and it was found that while the introduction of friction does not change the nanoindentation load–displacement relationship, it changes the indent surface pile-up profiles. The friction-free contact condition is assumed between the indenter and thin film surface based on Liu’s [41] researches. The indenter is gradually driven into Ag thin film by displacement-imposed boundary conditions. The indentation depth is increased by 0.01 nm at each load step. After each step, a quasi-Newton solver is used to iteratively minimize the total potential energy and to identify the equilibrium configuration of the system subjected to the new load step boundary conditions. The top, left and right surface of the film are left free, and the bottom surface is fixed on a rigid support throughout the simulation. The boundary effect in MD simulation can be effectively eliminated because the maximum indenter width and indentation depth are only two percent of the width and thickness of the film, respectively.
is the spacing between the adjacent (111) planes), respectively. The effect of coefficient of friction on the nanoindentation behavior of single crystal copper has been investigated by Liu et al. [41], and it was found that while the introduction of friction does not change the nanoindentation load–displacement relationship, it changes the indent surface pile-up profiles. The friction-free contact condition is assumed between the indenter and thin film surface based on Liu’s [41] researches. The indenter is gradually driven into Ag thin film by displacement-imposed boundary conditions. The indentation depth is increased by 0.01 nm at each load step. After each step, a quasi-Newton solver is used to iteratively minimize the total potential energy and to identify the equilibrium configuration of the system subjected to the new load step boundary conditions. The top, left and right surface of the film are left free, and the bottom surface is fixed on a rigid support throughout the simulation. The boundary effect in MD simulation can be effectively eliminated because the maximum indenter width and indentation depth are only two percent of the width and thickness of the film, respectively.
Choice of the Nanoindentation Orientation
To investigate the influence caused by crystalline anisotropy on nanoindentation process, it is very important to reasonably select a representative crystal orientation. However, the choice of the orientation in most of the literature, such as Chen and Shen [42] is primarily based on whether the results have any new characteristic, rather than intrinsic relationship between crystal structures. The nanoindentation orientations based on the FCC crystal structure characteristics are chosen in the present study. Figure 2a shows the slip systems of an FCC lattice, where the triangle plane and arrow direction indicate the slip plane and sliding direction of FCC lattice, respectively. There are eight triangle planes, in which the four upper planes diagonally parallel the four lower, and form four independent slip planes shown in Fig. 2a. These independent slip planes belong to the {111} crystal planes family. Since there are three favorable sliding directions in each slip plane, the twelve slip systems will be constituted. The deformation slip of crystal obeys Schmid’s criterion based on the dislocation theory [43]. When stress is applied to a crystal, shear stress is induced on the slip planes. The shear stress acting on the slip system increases with the increase of stress. When the shear stress reaches the shear yield stress, the slip system becomes active (such a slip system is termed as an “active slip system”) and the crystal begins to deform plastically. Therefore, the twelve slip systems shown in Fig. 2a play a key role in the deformation process of FCC crystal. The (111) slip plane is chosen as a study case because symmetries of the four independent slip planes exist. The schematic diagram of the various crystallographic orientations for nanoindentation is represented in Fig. 2b. Three different nanoindentation orientations are selected as follows:
Orientation I
Coordinate systems are taken as X[111],Y and Z
and Z for
for surface nanoindentation. The indenter is pushed into the
surface nanoindentation. The indenter is pushed into the surface with the indenter sides parallel to the (111) slip plane of Ag thin film. Along this orientation, there are two favorable slip directions, namely, slip direction (5) and (12) as shown in Fig. 2a.
surface with the indenter sides parallel to the (111) slip plane of Ag thin film. Along this orientation, there are two favorable slip directions, namely, slip direction (5) and (12) as shown in Fig. 2a.
Orientation II
Coordinate systems are taken as X[110],Y[001] and Z for (001) surface nanoindentation. The indenter is pushed into the (001) surface with a 35.7° angle between the indenter sides and the (111) slip plane of Ag thin film. Along this orientation, there are eight favorable slip directions, namely, slip direction (1), (2), (3), (4), (7), (8), (9) and (10) as shown in Fig. 2a.
for (001) surface nanoindentation. The indenter is pushed into the (001) surface with a 35.7° angle between the indenter sides and the (111) slip plane of Ag thin film. Along this orientation, there are eight favorable slip directions, namely, slip direction (1), (2), (3), (4), (7), (8), (9) and (10) as shown in Fig. 2a.
Orientation III
Coordinate systems are taken as X ,Y[111] and Z
,Y[111] and Z for (111) surface nanoindentation. The indenter is pushed into the (111) surface with the indenter sides perpendicular to the (111) slip plane of Ag thin film. Along this orientation, there are no favorable slip directions, as shown in Fig. 2a.
for (111) surface nanoindentation. The indenter is pushed into the (111) surface with the indenter sides perpendicular to the (111) slip plane of Ag thin film. Along this orientation, there are no favorable slip directions, as shown in Fig. 2a.
Results and Analysis
Nanoindentation on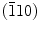 Surface
Surface
The load–displacement curve for nanoindentation into an Ag surface at the indenter width 8d is shown in Fig. 3. The load is obtained by dividing the total force on the indenter by the repeat distance in the out-of-plane direction of the thin film [29]. Then the units of load and displacement are given in Newton per meter and nanometer, respectively. Because the displacement-imposed boundary conditions are adopted during nanoindentation, the load–displacement curve shows obvious discontinuity and experiences abrupt drop several times, as the AB, CD and EF segments shown in Fig. 3. This is in good agreement with experimental results [44, 45]. Before the load reaches a peak value at point A, no slip system is active, which indicates that the thin film is deforming elastically. When the load reaches the critical load for initial defect nucleation (namely, point A on the curve of Fig. 3, for which the indentation depth and load are 0.54 nm and 20.30 N/m, respectively), the slip system becomes active, nucleation of dislocation begins and plastic deformation of the thin film is observed. Subsequently, the curve experiences an abrupt drop to point B. The contour plot of the out-of-plane displacement at point B is presented in Fig. 4a (the red spots represent the non-local atoms and the color legend displays the out-of-plane displacement). It can be seen from Fig. 4a that, with the increase of indentation depth, the severe stress concentration and lattice distortion happen in the regions on the right and left sides beneath the indenter tips. When the strain energy induced by lattice distortion is greater than the stacking fault (SF) energy of single crystal Ag, two SF planes are activated along the right and left sides of indenter (plotted by dashed lines in Fig. 4). Dislocations start to nucleate and subsequently emit into the thin film along the SF planes, thus the strain energy can be released. Once dislocations have been nucleated, the perfect dislocation rapidly dissociate into two Shockley partial dislocations (plotted by solid lines in Fig. 4) [29]. With further indentation, the load–displacement curve experiences the second and third abrupt drop at the CD and EF segments in Fig. 3, and then dislocation nucleation, emission and dissociation are accompanied, respectively [30–32]. Figure 4b shows the contour plot of the out-of-plane displacement of thin film at point F. Three dislocation dipoles along the SF planes are nucleated, emitted and subsequently dissociate into two Shockley partial dislocations in the whole nanoindentation processes.
surface at the indenter width 8d is shown in Fig. 3. The load is obtained by dividing the total force on the indenter by the repeat distance in the out-of-plane direction of the thin film [29]. Then the units of load and displacement are given in Newton per meter and nanometer, respectively. Because the displacement-imposed boundary conditions are adopted during nanoindentation, the load–displacement curve shows obvious discontinuity and experiences abrupt drop several times, as the AB, CD and EF segments shown in Fig. 3. This is in good agreement with experimental results [44, 45]. Before the load reaches a peak value at point A, no slip system is active, which indicates that the thin film is deforming elastically. When the load reaches the critical load for initial defect nucleation (namely, point A on the curve of Fig. 3, for which the indentation depth and load are 0.54 nm and 20.30 N/m, respectively), the slip system becomes active, nucleation of dislocation begins and plastic deformation of the thin film is observed. Subsequently, the curve experiences an abrupt drop to point B. The contour plot of the out-of-plane displacement at point B is presented in Fig. 4a (the red spots represent the non-local atoms and the color legend displays the out-of-plane displacement). It can be seen from Fig. 4a that, with the increase of indentation depth, the severe stress concentration and lattice distortion happen in the regions on the right and left sides beneath the indenter tips. When the strain energy induced by lattice distortion is greater than the stacking fault (SF) energy of single crystal Ag, two SF planes are activated along the right and left sides of indenter (plotted by dashed lines in Fig. 4). Dislocations start to nucleate and subsequently emit into the thin film along the SF planes, thus the strain energy can be released. Once dislocations have been nucleated, the perfect dislocation rapidly dissociate into two Shockley partial dislocations (plotted by solid lines in Fig. 4) [29]. With further indentation, the load–displacement curve experiences the second and third abrupt drop at the CD and EF segments in Fig. 3, and then dislocation nucleation, emission and dissociation are accompanied, respectively [30–32]. Figure 4b shows the contour plot of the out-of-plane displacement of thin film at point F. Three dislocation dipoles along the SF planes are nucleated, emitted and subsequently dissociate into two Shockley partial dislocations in the whole nanoindentation processes.
For the surface nanoindentation, the slip systems can be activated under a smaller external load and two parallel slip planes yield around the indenter tip. Subsequently, one can clearly observe the dislocation nucleation, emission and dissociation. The obvious discontinuity of load–displacement curve is the result of these dislocation activities.
surface nanoindentation, the slip systems can be activated under a smaller external load and two parallel slip planes yield around the indenter tip. Subsequently, one can clearly observe the dislocation nucleation, emission and dissociation. The obvious discontinuity of load–displacement curve is the result of these dislocation activities.
Nanoindentation on (001) Surface
Figure 5 shows the load–displacement curve for nanoindentation into an Ag (001) surface at the indenter width 8d, and the curve still shows obvious discontinuities. Point A in Fig. 5(for which the indentation depth and load are 0.55 nm and 10.79 N/m, respectively) is a critical point that denotes the beginning of elastic-to-plastic transition. The corresponding critical load for first dislocation emission is 10.79 N/m, which is 46.85% lower than that on surface. This decrease of critical load is found to be associated with the number of activated slip systems. Compared with the nanoindentation on
surface. This decrease of critical load is found to be associated with the number of activated slip systems. Compared with the nanoindentation on surface, the more favorable slip directions can be found along the nanoindentation orientation II(as shown in Fig. 2) and these slip systems can be activated under a very small external load, hence the critical load on (001) surface is smaller than that on
surface, the more favorable slip directions can be found along the nanoindentation orientation II(as shown in Fig. 2) and these slip systems can be activated under a very small external load, hence the critical load on (001) surface is smaller than that on surface.
surface.
After the plastic deformation occurs, the load–displacement curve still experiences load drop several times, as shown in Fig. 5 by the AB, CD, EF and GH segments. The von Mises strain distribution at points B, D, F and H is plotted in Fig. 6a–6d (the red spots represent the non-local atoms and the color legend displays the von Mises strain values), respectively. When the indentation depth is increased to 0.56 nm (corresponding to point B in Fig. 5), the first load drop occurs, and two SF planes are activated beneath the right and left sides of the indenter tip (plotted by dashed lines in Fig. 6a), which corresponds to the simultaneous nucleation of two Shockley partials beneath the indenter (shown by solid lines in Fig. 6a) in the (111) plane along the direction on the left-hand side and in the
direction on the left-hand side and in the plane along the
plane along the direction on the right-hand side, as seen in Fig. 6a. After dislocations nucleated, the two Shockley partials grow and intersect to form a dislocation lock (indicated in Fig. 6a by the region in red). With increasing load from the indenter, the dislocation lock remains intact and a wedge-shape region is constrained under the indenter by the two {111} slip planes, as seen in Fig. 6b. In addition, there are four slip planes on the left-hand side of the wedge that pass the lock and extend away from the surface. Accompanied by a second load drop (as the CD segment shown in Fig. 5), one twinning plane along the
direction on the right-hand side, as seen in Fig. 6a. After dislocations nucleated, the two Shockley partials grow and intersect to form a dislocation lock (indicated in Fig. 6a by the region in red). With increasing load from the indenter, the dislocation lock remains intact and a wedge-shape region is constrained under the indenter by the two {111} slip planes, as seen in Fig. 6b. In addition, there are four slip planes on the left-hand side of the wedge that pass the lock and extend away from the surface. Accompanied by a second load drop (as the CD segment shown in Fig. 5), one twinning plane along the direction is produced and the deformation twinning is represented in Fig. 6b.
direction is produced and the deformation twinning is represented in Fig. 6b.
When the indentation depth reaches 1.2 nm, two new slip planes on the lower left-hand side of the wedge are activated and then glide along the and
and directions, respectively, as seen in Fig. 6c. Subsequently, a new dislocation lock is produced under the lower left-hand side of the indenter. In order to pass this new dislocation lock, the two slip planes compete and suppress each other. The slip plane on the lower left-hand side of the wedge passes by the dislocation lock again and extends to a further distance along the
directions, respectively, as seen in Fig. 6c. Subsequently, a new dislocation lock is produced under the lower left-hand side of the indenter. In order to pass this new dislocation lock, the two slip planes compete and suppress each other. The slip plane on the lower left-hand side of the wedge passes by the dislocation lock again and extends to a further distance along the direction. Simultaneously, a second twinning plane is produced due to the appearance of cross-slip. Corresponding to the appearance of cross-slip, a third abrupt drop in the load–displacement curve is displayed. Figure 6d (corresponding to point H in Fig. 5) shows the von Mises distribution at the indentation depth of 1.80 nm. The severe lattice distortion is caused by the strong driving force of indenter. Furthermore, the orderly arrangement of atoms beneath the indenter is broken, which changed from order to disorder. As the lattice distortion becomes more severe, the number of distinct slip planes increases and these slip planes intertwine with one another. The glide directions are changed due to the severe lattice distortion, which no longer merely extend along the
direction. Simultaneously, a second twinning plane is produced due to the appearance of cross-slip. Corresponding to the appearance of cross-slip, a third abrupt drop in the load–displacement curve is displayed. Figure 6d (corresponding to point H in Fig. 5) shows the von Mises distribution at the indentation depth of 1.80 nm. The severe lattice distortion is caused by the strong driving force of indenter. Furthermore, the orderly arrangement of atoms beneath the indenter is broken, which changed from order to disorder. As the lattice distortion becomes more severe, the number of distinct slip planes increases and these slip planes intertwine with one another. The glide directions are changed due to the severe lattice distortion, which no longer merely extend along the direction, but glide along the
direction, but glide along the and
and directions by turns. In the meantime, both the deformation twinning and cross-slip are emerged. However, in Jin’s [37] numerical results, the cross-slip of dislocations was not be observed due to the shallow indentation depth. One can find that the nature of plastic deformation on (001) surface nanoindentation is collective dislocation activities, such as deformation twinning and cross-slip. The dislocation morphologies obtained by QC simulation are found to be quite similar to the experimental results [46], although the crystal material is not the same.
directions by turns. In the meantime, both the deformation twinning and cross-slip are emerged. However, in Jin’s [37] numerical results, the cross-slip of dislocations was not be observed due to the shallow indentation depth. One can find that the nature of plastic deformation on (001) surface nanoindentation is collective dislocation activities, such as deformation twinning and cross-slip. The dislocation morphologies obtained by QC simulation are found to be quite similar to the experimental results [46], although the crystal material is not the same.
For the (001) surface nanoindentation, the slip systems can be activated under a very small external load. A dislocation lock is noted to form during the glide process. These slip planes in order to pass the dislocation lock compete with each other and eventually extend along the predominant slip direction. During the nanoindentation, one can clearly observe the dislocation lock, deformation twinning and cross-slip. The load drop in the load–displacement curve is the result of the complex collective dislocation activities.
Nanoindentation on (111) Surface
Figure 7 shows the load–displacement curve for nanoindentation into an Ag (111) surface at the indenter width 8d. As compared with the nanoindentation on and (001) surfaces, although similar features in the load–displacement curve are observed, e.g. the curve shows obvious discontinuities and experiences abrupt drops on several occasions, the curve reflects entirely different dislocation activities, which can be confirmed by directly observing the atomic structure beneath the indenter (as shown in Fig. 8). It can be seen from Fig. 7 that the critical indentation depth and critical load (namely, point A on the curve of Fig. 7, for which the indentation depth and load are 1.03 nm and 39.80 N/m, respectively) on (111) surface is the largest among the three different nanoindentation orientations. The critical indentation depth and critical load on (111) surface are 47.57 and 48.99%, 46.60 and 72.89% higher than these on
and (001) surfaces, although similar features in the load–displacement curve are observed, e.g. the curve shows obvious discontinuities and experiences abrupt drops on several occasions, the curve reflects entirely different dislocation activities, which can be confirmed by directly observing the atomic structure beneath the indenter (as shown in Fig. 8). It can be seen from Fig. 7 that the critical indentation depth and critical load (namely, point A on the curve of Fig. 7, for which the indentation depth and load are 1.03 nm and 39.80 N/m, respectively) on (111) surface is the largest among the three different nanoindentation orientations. The critical indentation depth and critical load on (111) surface are 47.57 and 48.99%, 46.60 and 72.89% higher than these on and (001) surfaces, respectively. The above fact is attributed that there is no favorable slip direction for nanoindentation on (111) surface (as shown in Fig. 2), and no slip system can be directly activated. The atoms beneath the indenter tip are pushed toward the thin film and then severe stress concentration happens in the regions on the right and left sides beneath the indenter tip (as shown in Fig. 8a, the red spots represent the non-local atoms, both the size of red spot and color legend correspond to the von Mises strain value). The thin film enters the plastic deformation stage until the severe lattice distortion happened, hence the critical indentation depth and the critical load are higher.
and (001) surfaces, respectively. The above fact is attributed that there is no favorable slip direction for nanoindentation on (111) surface (as shown in Fig. 2), and no slip system can be directly activated. The atoms beneath the indenter tip are pushed toward the thin film and then severe stress concentration happens in the regions on the right and left sides beneath the indenter tip (as shown in Fig. 8a, the red spots represent the non-local atoms, both the size of red spot and color legend correspond to the von Mises strain value). The thin film enters the plastic deformation stage until the severe lattice distortion happened, hence the critical indentation depth and the critical load are higher.
With the increase of indentation depth, the load–displacement curve experiences load drop several times, as the AB, CD and EF segments shown in Fig. 7, in which the amplitude of the first load drop is largest among these load drops in above three load–displacement curves. The atomic structure beneath the indenter at points B, D and F are plotted in Fig. 8b–d, respectively. It can be seen from Fig. 8b that the slip systems cannot be directly activated along this nanonindentation orientation without favorable slip directions. The crystal lattice beneath the indenter undergoes severe distortion and rotation under the action of external load. Subsequently, two new favorable slip directions along the [011] and the directions, respectively, are formed and then the glide starts. Figure 8c gives the atomic structure beneath the indenter at the indentation depth of 1.44 nm (corresponding to point D in Fig. 7). It is noted that if the dislocations glide along the
directions, respectively, are formed and then the glide starts. Figure 8c gives the atomic structure beneath the indenter at the indentation depth of 1.44 nm (corresponding to point D in Fig. 7). It is noted that if the dislocations glide along the direction are hampered, the slip direction will be reversed (from the
direction are hampered, the slip direction will be reversed (from the to the [110] direction) that results in the release of strain energy and a second load drops at CD segment in Fig. 7. With the aggravation of lattice distortion, a lot of strain energy is stored in the lattice, but these strain energy cannot be released at once because the glides along
to the [110] direction) that results in the release of strain energy and a second load drops at CD segment in Fig. 7. With the aggravation of lattice distortion, a lot of strain energy is stored in the lattice, but these strain energy cannot be released at once because the glides along , [110] and [011] directions are fully hampered. Therefore, new slip planes along the
, [110] and [011] directions are fully hampered. Therefore, new slip planes along the direction will be produced (as shown in Fig. 8d) in order that the strain energy can be rapidly released, which corresponds to the third abrupt drop of the load–displacement curve at EF segment in Fig. 7.
direction will be produced (as shown in Fig. 8d) in order that the strain energy can be rapidly released, which corresponds to the third abrupt drop of the load–displacement curve at EF segment in Fig. 7.
For the (111) surface nanoindentation, the slip surfaces cannot be directly activated. The crystal lattice beneath the indenter at the beginning of nanoindentation undergoes severe distortion and rotation under the action of external load, then the favorable slip directions can be formed and the glide starts. A lot of strain energy is stored in the lattice due to the severe lattice distortion and rotation. The load–displacement curve represents abrupt drop when this strain energy is rapidly released.
Discussion
Hardness
At present, Oliver-Pharr (O–P) method developed by Oliver and Pharr in 1992 has been widely adopted to calculate the hardness in the majority of commercial nanoindentation tester [4]. Nanoindentation hardness based on O–P method can be defined as

where Pmax and A are the peak load and the projected contact area, respectively. Combining the QC simulation results with the O–P method, hardness versus indenter width curves for nanoindentation on various crystallographic surfaces are represented in Fig. 9. It is clear that the hardness for a specified crystallographic surface is decreased as the indentation depth is increased, which shows strong indentation size effect. This is in agreement with the experimental results of Abu Al-Rub and Voyiadjis [47]. Although the hardnesses for nanoindentation on various crystallographic surfaces show the similar indentation size effect, the crystalline anisotropy still has a significant influence on hardness. When the width of indenter is 0.9445 nm (namely, 4d), the hardnesses for nanoindentation on  , (001) and (111) surfaces are 30.996, 16.378 and 56.237 GPa, respectively; whereas the width of indenter is 4.7227 nm (namely, 20d), the hardness for nanoindentation on
, (001) and (111) surfaces are 30.996, 16.378 and 56.237 GPa, respectively; whereas the width of indenter is 4.7227 nm (namely, 20d), the hardness for nanoindentation on  , (001) and (111) surfaces are 12.624, 8.110 and 30.345 GPa, respectively. The hardnesses for the (111) surface nanoindentation are always the largest; on the contrary, the hardnesses for the (001) surface nanoindentation are always the smallest. The calculated hardnesses of single crystal Ag thin film agree well with the experimental data [48].
, (001) and (111) surfaces are 12.624, 8.110 and 30.345 GPa, respectively. The hardnesses for the (111) surface nanoindentation are always the largest; on the contrary, the hardnesses for the (001) surface nanoindentation are always the smallest. The calculated hardnesses of single crystal Ag thin film agree well with the experimental data [48].
A significant difference exists in the hardnesses for nanoindentation on various crystallographic surfaces, which can be attributed to the anisotropy of lattice orientation. The slip systems for the (001) and the surfaces nanoindentation can be activated under a smaller external load with favorable slip directions (as shown in Fig. 2), thus the calculated hardness values are lower. Whereas the slip systems for the (111) surface cannot be directly activated at the outset of nanoindentation without favorable slip directions (as shown in Fig. 2), the calculated hardness values are the highest because the crystal lattice beneath the indenter first undergoes severe distortion and forms the favorable slip directions and subsequently starts their glide under the action of intense external load.
surfaces nanoindentation can be activated under a smaller external load with favorable slip directions (as shown in Fig. 2), thus the calculated hardness values are lower. Whereas the slip systems for the (111) surface cannot be directly activated at the outset of nanoindentation without favorable slip directions (as shown in Fig. 2), the calculated hardness values are the highest because the crystal lattice beneath the indenter first undergoes severe distortion and forms the favorable slip directions and subsequently starts their glide under the action of intense external load.
Contact Stress Distribution Under the Indenter
In order to elucidate the mechanisms of dislocation nucleation and interaction, we adapt the criterion derived by Rice and Thomson [49, 50] for dislocation nucleation. It is assumed that dislocation nucleation occurs when the distance between the dislocation and indenter is equal to the dislocation core radius. There are two forces acting on this dislocation, in which one is the Peach-Koehler force (FL) due to the indenter stress field driving the dislocation into the bulk, and the other is the image force (FI) pulling the dislocation to the surface. The competition between the two forces imply that if the dislocation is too close to the surface, it will be attracted to the surface, while if the dislocation is at a sufficient depth, it will propagate into the solid.
According to the R-T dislocation model, we introduce Volterra dislocations at x = ±a,y = h(x,y and z coordinate axes are shown in Fig. 1) and the dislocations are in equilibrium. Then, the force acting on the dislocation can be written as

where a is half-width of indenter,h is a distance between the dislocation and surface at which the dislocation is in equilibrium,b is the Burgers vector module and σ
xy
is the total shear stress acting on the dislocation, which is composed of two contributions. The one contribution ( ) arises from the indenter load which tries to push the dislocation away from the surface. The other contribution (
) arises from the indenter load which tries to push the dislocation away from the surface. The other contribution ( ) due to the image force of the dislocation pulls the dislocation toward the surface. The stress due to the indenter can be written as [51]
) due to the image force of the dislocation pulls the dislocation toward the surface. The stress due to the indenter can be written as [51]

where σ(x) and τ(x) are the normal and shear contact stress acting on the film due to the indenter. For a rigid, friction-free indenter, the normal and shear contact stress have the forms [51]


where P is the force per unit length exerted by the indenter, ν is Poisson’s ratio of the thin film. Here, P in Eq. (4) can be obtained from the QC simulations and a can be determined from the nanoindentation models in Fig. 1. Using Eqs. (4) and (5), we can get the contact stress distribution under the indenters.
Figure 10a–10c shows the normal contact stress distribution under the indenters for nanoindentation on , (001) and (111) surfaces at the indentation depth of 1.1 nm, respectively. It can be seen that the QC simulation results are in good agreement with the R-T dislocation model solution. For the same indenter size, the minimum normal contact stress appears at the center of indenter (namely, at x = 0 nm) and increases from the center to both sides of indenter. And finally, the strong stress concentration will be presented at the both sides of indenter, as shown in Fig. 10a. In addition, the normal contact stress decreases with the increase of the indenter widths (i.e. at x = 0.24 nm, the normal contact stress under the action of indenter width 4d, 8d, 12d, 16d and 20d are 7.91, 6.83, 4.57, 4.10 and 4.05 GPa, respectively). Figure 10b shows the normal contact stress distribution under the indenters for nanoindentation on (001) surface. Compared Fig. 10a with Fig. 10b, the similar features in the normal contact stress distribution can be noted. The normal contact stress distribution for nanoindentation on (111) surface is shown in Fig. 10c. At the same indenter size, the curves present the similar features with nanoindentation on
, (001) and (111) surfaces at the indentation depth of 1.1 nm, respectively. It can be seen that the QC simulation results are in good agreement with the R-T dislocation model solution. For the same indenter size, the minimum normal contact stress appears at the center of indenter (namely, at x = 0 nm) and increases from the center to both sides of indenter. And finally, the strong stress concentration will be presented at the both sides of indenter, as shown in Fig. 10a. In addition, the normal contact stress decreases with the increase of the indenter widths (i.e. at x = 0.24 nm, the normal contact stress under the action of indenter width 4d, 8d, 12d, 16d and 20d are 7.91, 6.83, 4.57, 4.10 and 4.05 GPa, respectively). Figure 10b shows the normal contact stress distribution under the indenters for nanoindentation on (001) surface. Compared Fig. 10a with Fig. 10b, the similar features in the normal contact stress distribution can be noted. The normal contact stress distribution for nanoindentation on (111) surface is shown in Fig. 10c. At the same indenter size, the curves present the similar features with nanoindentation on and (001) surfaces. The normal contact stress under the indenter is no longer decreased with the increase of the indenter widths, but presents an obvious change (i.e. at x = 0.24 nm, the normal contact stress under the action of indenter width 4d, 8d, 12d, 16d and 20d are 10.83, 5.96, 3.96, 9.10 and 7.50 GPa, respectively), which may be attributed to the different dislocation activities during nanoindentation. From what is discussed earlier, we can find that the normal contact stress distribution is very sensitive to indenter size.
and (001) surfaces. The normal contact stress under the indenter is no longer decreased with the increase of the indenter widths, but presents an obvious change (i.e. at x = 0.24 nm, the normal contact stress under the action of indenter width 4d, 8d, 12d, 16d and 20d are 10.83, 5.96, 3.96, 9.10 and 7.50 GPa, respectively), which may be attributed to the different dislocation activities during nanoindentation. From what is discussed earlier, we can find that the normal contact stress distribution is very sensitive to indenter size.
Figure 11a–11c shows the shear contact stress distribution under the indenters for nanoindentation on , (001) and (111) surfaces at the indentation depth of 1.1 nm, respectively. It can be seen that the QC simulation results are in good agreement with R-T dislocation model solution. The shear contact stress distribution for nanoindentation on three different surfaces shows the similar features, as seen in Fig. 11. At the same indenter size, the shear contact stress for nanoindentation on
, (001) and (111) surfaces at the indentation depth of 1.1 nm, respectively. It can be seen that the QC simulation results are in good agreement with R-T dislocation model solution. The shear contact stress distribution for nanoindentation on three different surfaces shows the similar features, as seen in Fig. 11. At the same indenter size, the shear contact stress for nanoindentation on , (001) and (111) surfaces at the center of indenter (namely, at x = 0 nm) is zero and slowly increases from the center to both sides of indenter (the positive and negative values represent the rightward and leftward direction of shear contact stress, respectively). Finally, the strong stress concentration will be presented at the both sides of indenter. In addition, the shear contact stress slowly decreases with the increase of the indenter widths. The shear contact stress distribution is very sensitive to indenter size, just as the normal contact stress distribution under the indenter.
, (001) and (111) surfaces at the center of indenter (namely, at x = 0 nm) is zero and slowly increases from the center to both sides of indenter (the positive and negative values represent the rightward and leftward direction of shear contact stress, respectively). Finally, the strong stress concentration will be presented at the both sides of indenter. In addition, the shear contact stress slowly decreases with the increase of the indenter widths. The shear contact stress distribution is very sensitive to indenter size, just as the normal contact stress distribution under the indenter.
To further clarify the effect of crystalline anisotropy on the contact stress distribution during nanoindentation processes, both the normal and shear contact stress distribution under the indenter for nanoindentation on various crystallographic surfaces are shown in Fig. 12, where the indenter width is 16d and the indentation depth is 1.1 nm. It can be seen that the crystalline anisotropy has a significant influence on contact stress distribution at the same indentation depth and indenter width. Both the normal and shear contact stress under the indenters for nanoindentation on (111) surface are the largest, while they are the lowest on the (001) surface. This difference is associated with the FCC crystal structure characteristics. Along the and the [001] directions, the slip systems are easy to activate with favorable slip directions, thus both the normal and the shear contact stress under the indenters are smaller. Whereas the slip systems along the [111] direction are hard to active without favorable slip directions, both the normal and shear contact stress under the indenters are larger.
and the [001] directions, the slip systems are easy to activate with favorable slip directions, thus both the normal and the shear contact stress under the indenters are smaller. Whereas the slip systems along the [111] direction are hard to active without favorable slip directions, both the normal and shear contact stress under the indenters are larger.
Critical Load for First Dislocation Emission
The critical load for first dislocation emission is an important parameter in nanoindentation, which not only reflects the intrinsic property of dislocation nucleation in the thin film, but also infers the elastic-to-plastic transition mechanism during nanoindentation.
The shear stress on the slip planes can be readily computed by using the expressions for traction in Eq. (3). When for the friction-free indenter, Eq. (3) can be simplified as
for the friction-free indenter, Eq. (3) can be simplified as

The stress on the dislocation at x = ±a,y = h due to its image force can be shown to be

where μ is the shear modulus. From Eq. (7), the dislocation very close to the surface (namely,h is very small) will be pulled to the surface by its image force and the dislocation far from the surface (namely,h is very large) will be pushed further into the thin film. It implies that there is an intermediate distance, assumed to be h0, at which the dislocation remains in equilibrium, such that:

From the R-T dislocation model strategy, when this distance is equal to the dislocation core radius, it is assumed that nucleation occurs. By combining Eqs. (6)–(8) and letting h0 = rc, the critical load Pc r for dislocation nucleation under the friction-free indenter is

Because of , Eq. (9) can be simplified as
, Eq. (9) can be simplified as

Where , the parameter KR-T in the R-T dislocation model depends on the dislocation core radius rc. From Eq. (10), one can conclude that the critical load for first dislocation emission is in direct proportion with the square root of the indenter half-width.
, the parameter KR-T in the R-T dislocation model depends on the dislocation core radius rc. From Eq. (10), one can conclude that the critical load for first dislocation emission is in direct proportion with the square root of the indenter half-width.
Figure 13 shows the critical load for first dislocation emission versus indenter width curves for nanoindentation on various crystallographic surfaces. It is obvious that the crystalline anisotropy and indenter size play an important role in measuring the critical load. At the same indenter size, nanoindentation on (111) surface requires the largest critical load, while nanoindentation on (001) surface requires the lowest (i.e. when the indenter width is 2.834 nm (namely, 12d), the critical load on (001), and (111) surfaces are 13.09 N/m, 24.63 N/m and 50.85 N/m, respectively). At the same crystallographic surface, the critical load is increased as indenter widths is increased (i.e. for the
and (111) surfaces are 13.09 N/m, 24.63 N/m and 50.85 N/m, respectively). At the same crystallographic surface, the critical load is increased as indenter widths is increased (i.e. for the surface nanoindentation, the critical loads under the action of indenter width 4d, 8d, 12d, 16d and 20d are 14.64 N/m, 20.30 N/m, 24.63 N/m, 28.31 N/m and 29.81 N/m, respectively). In addition, it is in direct proportion to the square root of the indenter half-width, which is in accordance with R-T dislocation model solution.
surface nanoindentation, the critical loads under the action of indenter width 4d, 8d, 12d, 16d and 20d are 14.64 N/m, 20.30 N/m, 24.63 N/m, 28.31 N/m and 29.81 N/m, respectively). In addition, it is in direct proportion to the square root of the indenter half-width, which is in accordance with R-T dislocation model solution.
Strain Energy
In general, the nanoindentation in a metal thin film results in a high local dislocation density beneath the indenter and stores large amounts of strain energy, which increases with deformation process due to the severe lattice distortion in the thin film. We analyzed and compared the nanoindentation deformation processes on various crystallographic surfaces to further investigate the effect of crystalline anisotropy on the strain energy. The strain energy versus displacement curves for nanoindentation on various crystallographic surfaces at the indenter width 8d are shown in Fig. 14(the units of strain energy is given in eV). It is worth noting that there is a distinct effect on system strain energy due to crystalline anisotropy, for instance, the strain energy of nanoindentation on (111) surface is the largest, while that of nanoindentation on (001) surface is the lowest. This difference of strain energy can be attributed to the entirely different dislocation activities triggered by nanoindentation on three different surfaces. Although the strain energy curves obtained from nanoindentation on various crystallographic surfaces exhibit different features, they show a similar behavior in which the strain energy increases as the indentation depth becomes larger. Compared the load–displacement curves (as shown in Figs. 3–5) with the corresponding strain energy curves (as shown in Fig. 14), it can be seen that the load–displacement curve and the corresponding strain energy curve have similar variations for the same crystallographic surface and indenter width, for example, the rise or drop in the load–displacement curves correspond to the increase or decrease of their strain energy. The corresponding relationship between load–displacement curve and strain energy curve is still related to the dislocation activities. When the dislocations are activated by the indenter stress field, the lattice distortion is inevitable and the system strain energy will increase.
Conclusions
In this paper, the nature of crystalline anisotropy and indenter size on the onset of plasticity during nanoindentation without boundary effect are investigated with deep indentation depth by QC method. The major conclusions of this work can be summarized as follows:
-
(1)
The obvious discontinuity in load–displacement curves is closely related to the entirely different dislocation activities triggered by nanoindentation on various surfaces, which correspond to the dislocation nucleation and emission for nanoindentation on
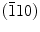 surface, deformation twinning and cross-slip for nanoindentation on (001) surface, and lattice distortion and rotation for nanoindentation on (111) surface. The results obtained by QC simulation show quite similar dislocation morphologies to the experimental results.
surface, deformation twinning and cross-slip for nanoindentation on (001) surface, and lattice distortion and rotation for nanoindentation on (111) surface. The results obtained by QC simulation show quite similar dislocation morphologies to the experimental results. -
(2)
A distinct effect of crystalline anisotropy and indenter size are found on hardness. At the nanoindentation along the crystal orientation with more favorable slip directions, the corresponding hardness will decrease; whereas that will increase at the nanoindentation along the crystal orientation with less or without favorable slip directions. The calculated hardnesses of the thin film agree well with the experimental data.
-
(3)
The contact stress distribution under the indenter is very sensitive to indenter size and crystalline anisotropy. Along the orientation that the slip systems are easy to be activated, both the normal and shear contact stress are small; on the contrary, they are large along the orientation that the slip systems are hard to be activated.
-
(4)
Crystalline anisotropy and indenter size play an important role in measuring the critical load for first dislocation emission. At the same indenter size, the nanoindentation on (111) surface requires the largest critical load, while the nanoindentation on (001) surface requires the lowest. At the same crystallographic surface, the critical loads are increased as indenter widths are increased. In addition, they are in direct proportion to the square root of the indenters’ half-width, which is in good agreement with R-T dislocation model solution.
-
(5)
The strain energy of nanoindentation on (111) surface is the largest, while that of nanoindentation on (001) surface is the lowest. Although these strain energy curves for nanoindentation on various crystallographic surfaces exhibit difference, they show a similar increasing tendency. At the same crystallographic surface and indenter width, there is a corresponding relationship between load–displacement curve and strain energy.
References
Siegel RW, Fougere GE: Nanostruct. Mater.. 1995, 6: 205. COI number [1:CAS:528:DyaK2MXmtleqs7c%3D] 10.1016/0965-9773(95)00044-5
Wang Y, Chen M, Zhou F, Ma E: Nature. 2002, 419: 912. COI number [1:CAS:528:DC%2BD38Xot1Klur8%3D]; Bibcode number [2002Natur.419..912W] 10.1038/nature01133
Valiev R: Nat. Mater.. 2004, 3: 511. COI number [1:CAS:528:DC%2BD2cXmtVOhs7k%3D]; Bibcode number [2004NatMa...3..511V] 10.1038/nmat1180
Oliver WC, Pharr GM: J. Mater. Res.. 1992, 7: 1564. COI number [1:CAS:528:DyaK38XktlWqtb4%3D]; Bibcode number [1992JMatR...7.1564O] 10.1557/JMR.1992.1564
Bhushan B, Koinkar VN: Appl. Phys. Lett.. 1994, 64: 1653. COI number [1:CAS:528:DyaK2cXivVKhtLw%3D]; Bibcode number [1994ApPhL..64.1653B] 10.1063/1.111949
Chen J, Bull SJ: Thin Solid Films. 2006, 494: 1. COI number [1:CAS:528:DC%2BD2MXht1aqsbnP]; Bibcode number [2006TSF...494....1C] 10.1016/j.tsf.2005.08.176
Viassak JJ, Nix WD: J. Mech. Phys. Solids. 1994, 42: 1223. Bibcode number [1994JMPSo..42.1223V] Bibcode number [1994JMPSo..42.1223V] 10.1016/0022-5096(94)90033-7
Kiely JD, Houston JE: Phys. Rev. B. 1998, 57: 12588. COI number [1:CAS:528:DyaK1cXjtFSmtbo%3D]; Bibcode number [1998PhRvB..5712588K] 10.1103/PhysRevB.57.12588
Kim JY, Kang SK, Greer JR, Kwon D: Acta Mater.. 2008, 56: 3338. COI number [1:CAS:528:DC%2BD1cXovFyhtL4%3D] 10.1016/j.actamat.2008.02.049
Shim S, Bei H, George EP, Pharr GM: Scr. Mater.. 2008, 59: 1095. COI number [1:CAS:528:DC%2BD1cXhtFSqs7rJ] 10.1016/j.scriptamat.2008.07.026
Zimmerman JA, Kelchner CL, Klein PA, Hamilton JC, Foiles SM: Phys. Rev. Lett.. 2001, 87: 165507. COI number [1:STN:280:DC%2BD3MnjslGnsQ%3D%3D]; Bibcode number [2001PhRvL..87p5507Z] 10.1103/PhysRevLett.87.165507
Shankar RM: Appl. Phys. Lett.. 2007, 90: 171924. Bibcode number [2007ApPhL..90R1924S] Bibcode number [2007ApPhL..90R1924S] 10.1063/1.2733027
Nowak R, Li CL, Maruno S: J. Mater. Res.. 1997, 12: 64. COI number [1:CAS:528:DyaK2sXisFyjsLo%3D]; Bibcode number [1997JMatR..12...64N] 10.1557/JMR.1997.0011
Soifer YM, Verdyan A, Kazakevich M, Rabkin E: Scr. Mater.. 2002, 47: 799. COI number [1:CAS:528:DC%2BD38XnvFOgs7g%3D] 10.1016/S1359-6462(02)00284-1
Jarausch KF, Kiely JD, Houston JE, Russell PE: J. Mater. Res.. 2000, 15: 1693. COI number [1:CAS:528:DC%2BD3cXlsFOltbo%3D]; Bibcode number [2000JMatR..15.1693J] 10.1557/JMR.2000.0244
Smith R, Christopher D, Kenny SD, Richter A, Wolf B: Phys. Rev. B. 2003, 67: 245405. Bibcode number [2003PhRvB..67x5405S] Bibcode number [2003PhRvB..67x5405S] 10.1103/PhysRevB.67.245405
Mirshams RA, Pothapragada RM: Acta Mater.. 2006, 54: 1123. COI number [1:CAS:528:DC%2BD28XnvVGjsQ%3D%3D] 10.1016/j.actamat.2005.10.048
Qin J, Huang Y, Hwang KC, Song J, Pharr GM: Acta Mater.. 2007, 55: 6127. COI number [1:CAS:528:DC%2BD2sXhtFGkt7fF] 10.1016/j.actamat.2007.07.016
Groenou V, Broese A, Kadijk SE: Acta Metall.. 1989, 37: 2613. 10.1016/0001-6160(89)90294-0
Khan MY, Brown LM, Chaudhri MM: J. Phys. D Appl. Phys.. 1992, 25: A257. COI number [1:CAS:528:DyaK38XhtFajs74%3D]; Bibcode number [1992JPhD...25A.257K] 10.1088/0022-3727/25/1A/039
Nix WD: Metall. Trans. A. 1989, 20A: 2217. COI number [1:CAS:528:DyaK3cXmtVOmuw%3D%3D]; Bibcode number [1989MTA....20.2217N]
Feng G, Nix WD: Scr. Mater.. 2004, 51: 599. COI number [1:CAS:528:DC%2BD2cXltlyhsro%3D] 10.1016/j.scriptamat.2004.05.034
Durst K, Backes B, Goken M: Scr. Mater.. 2005, 52: 1093. COI number [1:CAS:528:DC%2BD2MXisFaqtb0%3D] 10.1016/j.scriptamat.2005.02.009
Tsuru T, Shibutani Y: Phys. Rev. B. 2007, 75: 035415. Bibcode number [2007PhRvB..75c5415T] Bibcode number [2007PhRvB..75c5415T] 10.1103/PhysRevB.75.035415
Tadmor EB, Ortiz M, Phillips R: Phys. Mag. A. 1996, 73: 1529. Bibcode number [1996PMagA..73.1529T] Bibcode number [1996PMagA..73.1529T] 10.1080/01418619608243000
Shenoy VB, Miller R, Tadmor EB, Rodney D, Phillips R, Ortiz M: J. Mech. Phys. Solids. 1999, 47: 611. Bibcode number [1999JMPSo..47..611S] Bibcode number [1999JMPSo..47..611S] 10.1016/S0022-5096(98)00051-9
Shenoy VB, Phillips R, Tadmor EB: J. Mech. Phys. Solids. 2000, 48: 649. COI number [1:CAS:528:DC%2BD3cXisFSntL4%3D]; Bibcode number [2000JMPSo..48..649S] 10.1016/S0022-5096(99)00055-1
Ni YS, Wang HT: Chin. Q. Mech.. 2005, 26: 366. [in Chinese] [in Chinese]
Tadmor EB, Miller R, Phillips R: J. Mater. Res.. 1999, 14: 2233. COI number [1:CAS:528:DyaK1MXjs1yltb0%3D]; Bibcode number [1999JMatR..14.2233T] 10.1557/JMR.1999.0300
Li JW, Jiang WG: Acta Metall. Sin.. 2007, 43: 851. COI number [1:CAS:528:DC%2BD2sXhtFCns7fM] [in Chinese]
Jiang WG, Li JW, Su JJ, Tang JL: Acta Mech. Solida Sin.. 2007, 28: 375. COI number [1:CAS:528:DC%2BD2sXjs1WrsLY%3D] [in Chinese]
Ni YS, Wang HT: Chin. J. Mech. Eng.. 2007, 43: 101. [in Chinese] [in Chinese] 10.3901/JME.2007.08.101
Miller R, Ortiz M, Phillips R, Shenoy V, Tadmor EB: Eng. Fract. Mech.. 1998, 61: 427. 10.1016/S0013-7944(98)00047-2
Wang HT, Qin ZD, Ni YS, Zhang W: Trans. Nonferr. Met. Soc. Chin.. 2008, 18: 1164. COI number [1:CAS:528:DC%2BD1cXht1KqurnN] 10.1016/S1003-6326(08)60199-5
Wang HT, Qin ZD, Ni YS, Zhang W: Acta Phys. Sin.. 2009, 58: 1057. COI number [1:CAS:528:DC%2BD1MXltV2qt70%3D] [in Chinese]
Dupont V, Sansoz F: Acta Mater.. 2008, 56: 6013. COI number [1:CAS:528:DC%2BD1cXhsVSqtL3M] 10.1016/j.actamat.2008.08.014
Jin J, Shevlin SA, Guo ZX: Acta Mater.. 2008, 56: 4358. COI number [1:CAS:528:DC%2BD1cXhtVCqsbfM] 10.1016/j.actamat.2008.04.064
Prudhomme S, Bauman PT, Oden JT: Int. J. Multiscale Comput. Eng.. 2006, 4: 647. COI number [1:CAS:528:DC%2BD2sXmsVGmtLw%3D] 10.1615/IntJMultCompEng.v4.i5-6.60
Heino P, Hakkinen H, Kaski K: Europhys. Let.. 1998, 41: 273. COI number [1:CAS:528:DyaK1cXpvFCqsg%3D%3D]; Bibcode number [1998EL.....41..273H] 10.1209/epl/i1998-00142-5
Voter AF: The embedded atom method. In Intermetallic Compounds: Principles. Edited by: Westbrook JH, Fleischer RL. Wiley, New York; 1994.
Liu Y, Wang B, Yoshino M, Roy S, Lu H, Komanduri R: J. Mech. Phys. Solids. 2005, 53: 2718. COI number [1:CAS:528:DC%2BD2MXhtVKqtbbM]; Bibcode number [2005JMPSo..53.2718L] 10.1016/j.jmps.2005.07.003
Chen P, Shen Y: Int. J. Solids Struct.. 2008, 45: 6001. COI number [1:CAS:528:DC%2BD1cXhsFWgsLjM] 10.1016/j.ijsolstr.2008.07.008
Hirth JP, Lothe J: Theory of Dislocations. Wiley, New York; 1982.
Van Vliet KJ, Li J, Zhu T, Yip S, Suresh S: Phys. Rev. B. 2003, 67: 104105. Bibcode number [2003PhRvB..67j4105V] Bibcode number [2003PhRvB..67j4105V] 10.1103/PhysRevB.67.104105
Gouldstone A, Koh HJ, Zeng KY, Giannakopoulos AE, Suresh S: Acta Mater.. 2000, 48: 2277. COI number [1:CAS:528:DC%2BD3cXjt1Sisbk%3D] 10.1016/S1359-6454(00)00009-4
Yu HH, Shrotriya P, Gao YF, Kim KS: J. Mech. Phys. Solids. 2007, 55: 489. COI number [1:CAS:528:DC%2BD2sXosFGnuw%3D%3D]; Bibcode number [2007JMPSo..55..489Y] 10.1016/j.jmps.2006.09.003
Abu Al-Rub RK, Voyiadjis GZ: Int. J. Plast.. 2004, 20: 1139. 10.1016/j.ijplas.2003.10.007
Ma Q, Clarke DR: J. Mater. Res.. 1995, 10: 853. COI number [1:CAS:528:DyaK2MXks1ehtbk%3D]; Bibcode number [1995JMatR..10..853M] 10.1557/JMR.1995.0853
Rice JR, Thomson R: Phil. Mag.. 1974, 29: 73. COI number [1:CAS:528:DyaE2cXhsV2mur4%3D]; Bibcode number [1974PMag...29...73R] 10.1080/14786437408213555
Rice JR: J. Mech. Phys. Solids. 1992, 40: 239. COI number [1:CAS:528:DyaK3sXksFeqsrY%3D]; Bibcode number [1992JMPSo..40..239R] 10.1016/S0022-5096(05)80012-2
Johnson KL: Contact Mechanics. Cambridge University Press, Cambridge; 1985.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 10576010). The authors would like to thank Tadmor E.B. and Miller R. for helpful comments and suggestions during the multiscale simulations.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, J., Ni, Y., Wang, H. et al. Effects of Crystalline Anisotropy and Indenter Size on Nanoindentation by Multiscale Simulation. Nanoscale Res Lett 5, 420 (2010). https://doi.org/10.1007/s11671-009-9500-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11671-009-9500-x




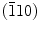 Surface
Surface
 surface at the indenter width 8d
surface at the indenter width 8d
 surface, where the indenter width is 8d
surface, where the indenter width is 8d





 surface, b(001) surface and c(111) surface at the indentation depth of 1.1 nm
surface, b(001) surface and c(111) surface at the indentation depth of 1.1 nm
 surface, b(001) surface andc c(111) surface at the indentation depth of 1.1 nm
surface, b(001) surface andc c(111) surface at the indentation depth of 1.1 nm


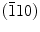 surface, deformation twinning and cross-slip for nanoindentation on (001) surface, and lattice distortion and rotation for nanoindentation on (111) surface. The results obtained by QC simulation show quite similar dislocation morphologies to the experimental results.
surface, deformation twinning and cross-slip for nanoindentation on (001) surface, and lattice distortion and rotation for nanoindentation on (111) surface. The results obtained by QC simulation show quite similar dislocation morphologies to the experimental results.