Abstract
Structural defects in monolayer molybdenum disulfide (MoS2) have significant influence on the electric, optical, thermal, chemical, and mechanical properties of the material. Among all the types of structural defects of the chemical vapor phase-grown monolayer MoS2, the VMoS3 point defect (a vacancy complex of Mo and three nearby S atoms) is another type of defect preferentially generated by the extended electron irradiation. Here, using the classical molecular dynamics simulation with reactive empirical bond-order (REBO) potential, we first investigate the effect of VMoS3 point defects on the elastic properties of monolayer MoS2 sheets. Under the constrained uniaxial tensile test, the elastic properties of monolayer MoS2 sheets containing VMoS3 vacancies with defect fraction varying from 0.01 to 0.1 are obtained based on the plane anisotropic constitutive relations of the material. It is found that the increase of VMoS3 vacancy concentration leads to the noticeable decrease in the elastic modulus but has a slight effect on Poisson’s ratio. The maximum decrease of the elastic modulus is up to 25 %. Increasing the ambient temperature from 10 K to 500 K has trivial influences on the elastic modulus and Poisson’s ratio for the monolayer MoS2 without defect and with 5 % VMoS3 vacancies. However, an anomalous parabolic relationship between the elastic modulus and the temperature is found in the monolayer MoS2 containing 0.1 % VMoS3 vacancy, bringing a crucial and fundamental issue to the application of monolayer MoS2 with defects.
Similar content being viewed by others
Background
The monolayer molybdenum disulfide (MoS2) is a graphene-like crystal with quasi-two-dimensional (2D) honeycomb lattice, consisting of a monatomic Mo-layer sandwiched between two monatomic S-layers. The pristine monolayer MoS2 holds many remarkable physical and chemical properties for its intrinsic direct bandgap of 1.8 eV [1] and high elastic modulus of ~0.2 TPa, which strongly promises for burgeoning 2D nanodevices, including transistor [2], field-effect transistor [3], phototransistors [4], nanomechanical resonator [5], and photodetector [6]. However, the structural defects can be commonly observed [7, 8] or deliberately introduced [9] in the monolayer MoS2, which have significant influence on its electrical conductivity [10], electrical contacts [11], band-to-band tunneling [12], catalytic [13], photoluminescence [14], magnetism [15], and thermal conductivity [16].
Structural defects, nine types of point defects (including vacancies and antisite defects), have been recently defined and characterized via atomic resolution imaging and first-principle calculation [7, 8]. The monosulfur vacancy (VS) is the most common point defect, frequently observed in experiments for its lowest formation energy (1.1 eV) [7]. So far, there are few documents concerning its impacts on the mechanical properties [17, 18], which can be momentous in MoS2 engineering applications. Dang and Spearot [17] conducted molecular dynamics (MD) nanoindentation simulations to investigate the VS effect on the mechanical behavior of monolayer MoS2. They revealed that the VS defects weaken the breaking force and induce displacive phase transformations under indentation. Gan and Zhao [18] performed first-principle calculations to show that the chirality effect on the mechanical properties of monolayer MoS2 becomes more and more significant with the increasing of strain, regardless of vacancies. Besides VS, VMoS3 (a vacancy complex of Mo and three nearby S atoms) is another type of defect preferentially generated by the extended electron irradiation [7]. However, there is still a lack of reports on the VMoS3 effect on the mechanical properties of monolayer MoS2.
Hence, in this letter, the mechanical properties of monolayer MoS2 containing VMoS3 (V-MoS2) with defect fraction from 0.01 to 0.1 are first investigated under the constrained uniaxial tensile test (CUATT) using MD simulation with reactive empirical bond-order (REBO) potential [19–21]. The REBO interatomic potential has been recently utilized to calculate the breaking force of monolayer MoS2 with VS defects [17] and has been demonstrated to be more effective in simulating the elastic behavior of monolayer MoS2 [22] than other interatomic potentials such as consistent valence force field (CVFF) and Stillinger-Weber (SW), under a small deformation (tensile strain ε < 5 %). Under the CUATT, the elastic properties of monolayer MoS2 sheets containing VMoS3 vacancies with defect fraction varying from 0.01 to 0.1 are obtained based on the plane anisotropic constitutive relations of the material. From our simulation results, it is found that the increase of VMoS3 vacancy concentration leads to the noticeable decrease in the elastic modulus but has a slight effect on Poisson’s ratio. The maximum decrease of the elastic modulus is up to 25 %. Increasing the ambient temperature from 10 K to 500 K has trivial influence on the elastic modulus and Poisson’s ratio for the monolayer MoS2 without defect and with 5 % VMoS3 vacancies. However, an anomalous parabolic relationship between the elastic modulus and the temperature is found in the monolayer MoS2 containing 0.1 % VMoS3 vacancy, which is in conflict with the previous work using the SW potential [23] and bringing a crucial and fundamental issue to the application of monolayer MoS2 with defects.
Methods
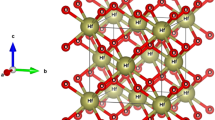
The LAMMPs [24] package is utilized to perform the MD simulations. A 2D periodic boundary condition is applied to the basal plane of MoS2 in order to eliminate the boundary effect and reproduce the inherent properties of monolayer MoS2 crystals. The height of the simulation box, normal to the basal plane, is set to far larger than the thickness of monolayer MoS2 (0.65 nm) [2] and is fixed during the simulation. To construct the VMoS3 vacancies, randomly specified Mo atoms are first deleted and the nearby three S atoms in the bottom S-layer are then carefully removed, especially the S atoms close to the periodic boundary. Increasing the defect fraction from 0.01 to 0.1, two or more neighboring Mo atoms are apt to be deleted together to form a large hole. And some irrational S atoms, without bonding to any Mo atoms, will occur in the upper S-layer and need to be definitely avoided. Figure 1 shows one of monolayer V-MoS2 sheets (10.97 × 12.67 nm2) with defect fraction of 0.08.
(a) the model of monolayer V-MoS2 sheet with 0.08 defect ratio. Red, green, and blue balls represent Mo, top-layer S, and bottom-layer S, respectively. (b) the top view of a VMoS3 vacancy and the direction of armchair 1 and zigzag 2 (top), the front view of a VMoS3 vacancy with missing dashed atoms (bottom)
Before performing the uniaxial tensile test using MD simulations, conjugate gradient energy minimizations are used to relax the orthorhombic simulation box as well as the atomic position of V-MoS2 sheets, to obtain the common initial configuration and the intrinsic elastic constants at absolute zero temperature (0 K). It is recently reported that the atomic relaxation has significant effects on the prediction of graphene’s elastic properties [25]. Accordingly, during the CUATT, the simulation cell length in the in-plane direction perpendicular to the applied strain keeps constant to exactly obtain the elastic constants of C ij (i, j = 1, 2 for the armchair and the zigzag direction, respectively, as shown in Fig. 1b). Considering the monolayer V-MoS2 as a 2D anisotropic material, we apply the 2D orthorhombic constitutive equation [26] to display the stress-strain relationship with the chirality effect, ignoring the shear stress and strain, given as
Herein, C ij can be expressed empirically in terms of engineering constants, modulus of elasticity E i and Poisson’s ratios ν ij (=−ε j /ε i ), as
and
Specially, C 11 = C 22 implies the 2D isotropic material. Furthermore, the engineering constants E i and v ij will be derived from the elastic constants of C ij after the CUATT. The intrinsic elastic constants of C ij are extracted from the slope of a perfect linear range of stress-strain curves. A strain increment of ∆ε = 5 × 10−5 is used among energy minimizations and following MD simulations [25].
Results and Discussion
Figure 2 shows the stress-strain curves of the defect-free MoS2 sheet (before creating the VMoS3 vacancies) subjected to the CUATT and the elastic constants obtained from the slope of perfect linear curves. According to Plimpton’s study [25], the deviation of the zigzag and armchair elastic moduli (E 1 = 215.76 GPa, E 2 = 214.59 GPa) results in the little chirality effect. The elastic moduli of the defect-free MoS2, E 1 and E 2, are consistent with the experimental results of Bertolazzi etal. (270 GPa) [27] and Cooper et al. (200 GPa) [28]. The abnormal disparity between C 12 and C 21 is presumably due to the computational error. This is because of C 12 supposed to be equal to C 21, in which the stiffness matrix of materials is symmetric. Therefore, the mean value of C 12 and C 21 is henceforth used to assess the mechanical properties of MoS2, regardless of vacancies.
In Fig. 3, we show the intrinsic engineering constants of V-MoS2 membranes versus the defect percentage at 0 K, compared with those of the perfect MoS2 sheet. E 1 and E 2 denote the elastic moduli with the armchair and zigzag directions, respectively. It is obvious that the effect of chirality on the elastic properties of V-MoS2 is negligible, regardless of the defect fraction. The V-MoS2 can be treated as isotropic 2D elastic materials due to the symmetric geometry of the VMoS3 vacancy. Increasing the defect fraction from 0 to 0.1, however, results in decreasing the elastic modulus E and Poisson’s ratio ν, with approximately linear relaxations. The value of elastic modulus drops obviously faster than that of Poisson’s ratio. The maximum reduction of elastic moduli is 25 %, larger than 5 % of Poisson’s ratio, which means that the impact of defect fraction on the elastic modulus is found to be more significant.
The thermal dependence of elastic properties of V-MoS2 is subsequently investigated with MD simulations, with a given defect fraction of 0.05 and under the temperature varying from 10 K to 500 K. Before the CUATT, the simulation box is relaxed for 20 ps with the NPT ensemble to bring the system to the desired temperature and pressure condition (0.1 bar). After the relaxation, the ensemble is switched to NVT, and the strain increment is applied via scaling the box length in the specified direction (zigzag for instance) and fixing the other orthogonal directions, to carry out the CUATT. The positions of system atoms are not remapped to the new box when the box is stretched, in order to keep the tensile stress consistent. In all MD simulations, the equations of motion are integrated by means of standard velocity - Verlet method with a 1-fs time step. The temperature and pressure conditions are controlled using the original Nose-Hoover thermostat and barostat.
In Fig. 4, we show the stress-strain curves of V-MoS2 with defect fraction of 0.05 under the armchair CUATT at 10 K and 300 K ambient conditions. The elastic constants of C 11 and C 21 at different temperatures are obtained by fitting the curves. The quality of the fit of the linear elastic model is expressed by the coefficient of determination R s. At 10 K, the value of R s is higher than 0.99, which means that the linear model could explain 99 % of the total variability within the range of values studied. However, the fluctuation at higher temperature reduces the value of R s down to 0.88 or even down to 0.78. Therefore, the divergence of elastic constants among the temperatures varying from 10 K to 500 K can be neglected, which demonstrates in Fig. 5 that temperatures lower than 500 K have basically little effect on the elastic properties (less than 5 %), including the elastic modulus and Poisson’s ratio, regardless of vacancies.
As shown in Fig. 5, Poisson’s ratio ν 12 (circles) and ν 21 (squares) of the defect-free MoS2 sheets slightly decrease as the temperature increases, excluding the data of ν 12 at 300 K and 400 K. However, Poisson’s ratio ν 12(diamonds) and ν 21 (stars) of V-MoS2 sheets slightly fluctuate as the temperature increases, in which the maximum amplitude does not exceed 2 %. The fluctuation can be attributed to the vacancies, which allow the ambient atoms to vibrate violently. As for Young’s modulus, the defect-free MoS2 sheet and the V-MoS2 sheet both show little dependence on the system temperature.
The temperature dependence of the defect-free MoS2 sheet obtained from our simulations with REBO potential is entirely contrary to the work of Zhao etal. [23] using the SW potential, in which Young’s modulus of perfect monolayer MoS2 obviously decreases with increasing the ambient temperature from 4.2 K to 500 K. They obtained the maximum reduction of Young’s modulus more than 30 %. However, the temperature dependence of the defect-free MoS2 with REBO potential in this paper is comparable to that of graphene [29], in which the maximum reduction of Young’s modulus is about 5 % when the system temperature increases from 300 K to 700 K. We believe that such result distinction is mainly derived from the adoption of different interatomic potentials and the processing procedure, as the co-worker of Zhao published another totally different result [30], in which Young’s modulus of perfect MoS2 is independent to the temperature range from 0 K to 300 K.
Recent experimental and theoretical nanoindentation studies have revealed that the low concentration of monovacancy leads to an anomalous remarkable stiffening effect on the graphene membrane [31–33]. Further simulation results [31] indicated that other types of point defects, such as divacancy, 555–777, and Stone-Wales defects, did not augment the in-plane stiffness of graphene but led to the ordinary degradation. As for the monolayer MoS2, which consists of stacks of S-Mo-S sandwiches, does the low fraction of VMoS3 vacancies lead to remarkable stiffening effect in a similar way? Considering that its crystal lattice and structural defects are distinct to those of graphene, a crucial and fundamental issue about the effect of low defect concentration on the mechanical properties of low dimensional nanomaterials is now brought up to scientists. Herein, we make a preliminary investigation on this issue. Constructing monolayer V-MoS3 sheet with defect fractions from 0.1 % to 1 %, we obtained the elastic modulus varying with defect fractions and temperatures from 1 K to 600 K. Surprisingly, the elastic modulus of monolayer MoS2 decreases monotonously as the defect fraction of VMoS3 increases, as shown in Fig. 6a. Moreover, the parabolic relationship between the elastic modulus of monolayer MoS2 containing 0.1 % VMoS3 vacancy and the temperature shows the anomalous temperature dependency of the elastic modulus of monolayer MoS2 with low concentration of VMoS3, as shown in Fig. 6b. However, note that there is a discrepancy in the testing method of mechanical properties between our results and those of literatures [31, 32]. We used uniaxial traction simulations instead of nanoindentation simulations. Hence, more comprehensive investigations combining the nanoindentation and uniaxial traction simulations are needed and now going on in our group, which will be submitted in the other manuscript.
Conclusions
In conclusion, we first investigate the mechanical properties and the thermal dependence of monolayer MoS2 containing VMoS3 vacancies with defect fraction varying from 0.01 to 0.1 under the constrained uniaxial tensile test using MD simulation with REBO potential. Our simulation results show that the VMoS3 vacancy concentration has noticeable influence on the elastic modulus but has a slight effect on Poisson’s ratio. Increasing the ambient temperature from 10 K to 500 K has trivial influence on the elastic modulus and Poisson’s ratio for the monolayer MoS2 without defect and with 5 % VMoS3 vacancies. However, an anomalous parabolic relationship between the elastic modulus and the temperature is found in the monolayer MoS2 containing 0.1 % VMoS3 vacancy and bringing a crucial and fundamental issue to the application of monolayer MoS2 with defects.
References
Mak KF, Lee C, Hone J, Shan J, Heinz TF (2010) Atomically thin MoS2: a new direct-gap semiconductor. Phys Rev Lett 105(13):136805
Radisavljevic B, Radenovic A, Brivio J, Giacometti V, Kis A (2011) Single-layer MoS2 transistors. Nat Nano 6(3):147–150
Li H, Yin Z, He Q, Li H, Huang X, Lu G et al (2012) Fabrication of single‐and multilayer MoS2 film‐based field‐effect transistors for sensing NO at room temperature. Small 8(1):63–67
Yin Z, Li H, Li H, Jiang L, Shi Y, Sun Y et al (2011) Single-layer MoS2 phototransistors. ACS Nano 6(1):74–80
Lee J, Wang Z, He K, Shan J, Feng PX-L (2013) High frequency MoS2 nanomechanical resonators. ACS Nano 7(7):6086–6091
Lopez-Sanchez O, Lembke D, Kayci M, Radenovic A, Kis A (2013) Ultrasensitive photodetectors based on monolayer MoS2. Nat Nanotechnol 8(7):497–501
Zhou W, Zou X, Najmaei S, Liu Z, Shi Y, Kong J et al (2013) Intrinsic structural defects in monolayer molybdenum disulfide. Nano Lett 13(6):2615–2622
Hong J, Hu Z, Probert M, Li K, Lv D, Yang X et al (2015) Exploring atomic defects in molybdenum disulphide monolayers. Nat Commun 6:6293
Komsa H-P, Kotakoski J, Kurasch S, Lehtinen O, Kaiser U, Krasheninnikov AV (2012) Two-dimensional transition metal dichalcogenides under electron irradiation: defect production and doping. Phys Rev Lett 109(3):035503
Ghorbani-Asl M, Enyashin AN, Kuc A, Seifert G, Heine T (2013) Defect-induced conductivity anisotropy in MoS2 monolayers. Phys Rev B 88(24):245440
Liu D, Guo Y, Fang L, Robertson J (2013) Sulfur vacancies in monolayer MoS2 and its electrical contacts. Appl Phys Lett 103(18):183113
Jiang X-W, Gong J, Xu N, Li S-S, Zhang J, Hao Y et al (2014) Enhancement of band-to-band tunneling in mono-layer transition metal dichalcogenides two-dimensional materials by vacancy defects. Appl Phys Lett 104(2):023512
Le D, Rawal TB, Rahman TS (2014) Single-layer MoS2 with sulfur vacancies: structure and catalytic application. J Phys Chem C 118(10):5346–5351
Nan H, Wang Z, Wang W, Liang Z, Lu Y, Chen Q et al (2014) Strong photoluminescence enhancement of MoS2 through defect engineering and oxygen bonding. ACS Nano 8(6):5738–5745
Tao P, Guo H, Yang T, Zhang Z (2014) Strain-induced magnetism in MoS2 monolayer with defects. J Appl Phys 115(5):054305
Ding Z, Pei Q-X, Jiang J-W, Zhang Y-W (2015) Manipulating the thermal conductivity of monolayer MoS2 via lattice defect and strain engineering. J Phys Chem C 119(28):16358–16365
Dang KQ, Spearot DE (2014) Effect of point and grain boundary defects on the mechanical behavior of monolayer MoS2 under tension via atomistic simulations. J Appl Phys 116(1):013508
Gan Y, Zhao H (2014) Chirality effect of mechanical and electronic properties of monolayer MoS2 with vacancies. Phys Lett A 378(38):2910–2914
Liang T, Phillpot SR, Sinnott SB (2009) Parametrization of a reactive many-body potential for Mo–S systems. Phys Rev B 79(24):245110
Liang T, Phillpot SR, Sinnott SB (2012) Erratum: Parametrization of a reactive many-body potential for Mo--S systems [Phys. Rev. B 79, 245110 (2009)]. Phys Rev B 85(19):199903
Stewart JA, Spearot D (2013) Atomistic simulations of nanoindentation on the basal plane of crystalline molybdenum disulfide (MoS2). Model Simul Mater Sci Eng 21(4):045003
Xiong S, Cao G (2015) Molecular dynamics simulations of mechanical properties of monolayer MoS2. Nanotechnology 26(18):185705
Zhao J, Jiang J-W, Rabczuk T (2013) Temperature-dependent mechanical properties of single-layer molybdenum disulphide: molecular dynamics nanoindentation simulations. Appl Phys Lett 103(23):231913
Plimpton S (1995) Fast parallel algorithms for short-range molecular dynamics. J Comput Phys 117(1):1–19
Gamboa A, Vignoles GL, Leyssale J-M (2015) On the prediction of graphene’s elastic properties with reactive empirical bond order potentials. Carbon 89:176–187
Gibson RF. Principles of composite material mechanics. United Stated of America: CRC press; 2011.
Bertolazzi S, Brivio J, Kis A (2011) Stretching and breaking of ultrathin MoS2. ACS Nano 5(12):9703–9
Cooper RC, Lee C, Marianetti CA, Wei X, Hone J, Kysar JW (2013) Nonlinear elastic behavior of two-dimensional molybdenum disulfide. Phys Rev B 87(3):035423
Shen L, Shen H-S, Zhang C-L (2010) Temperature-dependent elastic properties of single layer graphene sheets. Mater Des 31(9):4445–9
Jiang J, Park H (2014) Mechanical properties of MoS2/graphene heterostructures. Appl Phys Lett 105(3):033108
Kvashnin DG, Sorokin PB (2015) Mechanical properties of MoS2/graphene heterostructures. J Phys Chem Lett 6(12):2384–2387
Song Z, Xu Z (2016) Geometrical effect ‘stiffens’ graphene membrane at finite vacancy concentrations. Extreme Mechanics Letters 6:82–87
López-Polín G, Gómez-Navarro C, Parente V, Guinea F, Katsnelson M, Pérez-Murano F, Gómez-Herrero J (2015) Increasing the elastic modulus of graphene by controlled defect creation. Nat Phys 11(1):26–31
Acknowledgements
The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 50903017) and the Fujian Collaborative Innovation Center of High-End Manufacturing Equipment. MLL would like to thank the financial support from the China Scholarship Council during his visit to Rice University. The authors thanks Tao Liang for his support on the LAMMPs code of REBO potentials.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing Interests
The authors declare that they have no competing interests.
Authors’ Contributions
The simulation results were mainly analyzed by MLL and YCY. The simulation processes were originally conducted by MLL and LPT. YLW made the double check and revised all the simulation data. Some fairly helpful proposals about the construction of models were made by YCY and JL. All authors participated in the preparation of the manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, M., Wan, Y., Tu, L. et al. The Effect of VMoS3 Point Defect on the Elastic Properties of Monolayer MoS2 with REBO Potentials. Nanoscale Res Lett 11, 155 (2016). https://doi.org/10.1186/s11671-016-1377-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s11671-016-1377-x