Introduction

Ferroelectrics, which can convert mechanical to electrical energy (and vice versa) have wide applications in medical imaging, telecommunication and ultrasonic devices, the physical properties of which are sensitive to external conditions, such as strain, film thickness, temperature, electric and magnetic fields [1–3]. BaTiO3 (BTO) and PbTiO3 (PTO), as prototype ferroelectric materials and simple systems, have been intensively studied [4, 5]. It is known that the ferroelectricity arises from the competition of short-range repulsions which favor the paraelectric cubic phase and Coulomb forces, which favor the ferroelectric phase [6, 7]. As the pressure increases, the short-range repulsions increase faster than the Coulomb forces, leading to the reduced ferroelectricity. Accompanied with the suppression of ferroelectricity, the piezoelectricity decreases and even disappears. However, recent studies have shown that the noncollinear polarization rotation, occurring at phase transition pressure, can result in the giant piezoelectric response [8, 9]. In contrast to previous theoretical studies of the effects of epitaxial strain on the spontaneous polarization of ferroelectric thin films, we have systematically studied the influence of uniaxial and in-plane epitaxial strains on the mechanical and piezoelectric properties of perovskite ferroelectrics [10–15]. So far, there has been no previous work on the effect of uniaxial tensile strains on the mechanical and piezoelectric properties of short-period BTO/PTO superlattices.

Ferroelectric superlattices composed of alternating epitaxial oxides ultrathin layers are currently under intensive study due to their excellent ferroelectric and piezoelectric properties [16]. Ferroelectricity can be induced in superlattice in spite of the paraelectric nature of and . This is because the coincidence of the positive and negative charge centers is destroyed in the superlattice and electric dipoles are induced. Moreover, ferroelectricity can be enhanced in ferroelectric superlattices in certain stacking sequences [17]. The overall polarization of three-component SrTiO3(STO)/BTO/PTO ferroelectric superlattices can also be improved by increasing the number of BTO and PTO layers [18]. Thanks to the periodic nature, it is possible to study the effect of uniaxial or biaxial strains on the properties of ferroelectric superlattices from first principles.

In this work, we perform total energy as well as linear response calculations to study the effect of uniaxial tensile stress along the c axis on the mechanical and piezoelectric properties of short-period BTO/PTO superlattice. We show the mechanical properties by calculating the ideal tensile strength, elastic constants and valence charge density at different strains. We also show the influence of uniaxial stress on the piezoelectricity. To reveal the underlying mechanisms, we study the effects of uniaxial tensile stress on the atomic displacements and Born effective charges, respectively.

Computational Methods

Our calculations are performed within the local density approximation (LDA) to the density functional theory (DFT) as implemented in the plane-wave pseudopotential ABINIT package [19]. To ensure good numerical convergence, the plane-wave energy cutoff is set to be 80 Ry, and the Brillouin zone integration is performed with 6 × 6 × 6 k-meshpoints. The norm-conserving pseudopotentials generated by the OPIUM program are tested against the all-electron full-potential linearized augmented plane-wave method [20, 21]. The orbitals of Ba 5s25p66s2, Pb 5d106s26p2, Ti 3s23p63d24s2 and O 2s22p4 are explicitly included as valence electrons. The dynamical matrices and Born effective charges are computed by the linear response theory of strain type perturbations, which has been proved to be highly reliable for ground state properties [22–24]. The polarization is calculated by the Berry-phase approach [25]. The LDA is used instead of the generalized gradient approximation (GGA) because the GGA is found to overestimate both the equilibrium volume and strain for the perovskite structures [26]. The piezoelectric strain coefficients , where e is the piezoelectric stress tensor and the elastic compliance tensor s is the reciprocal of the elastic stiffness tensor c (Roman indexes from 1 to 3, and Greek ones from 1 to 6).

In the calculations, a double-perovskite ten-atom supercell along the c axis is used for the tetragonal short-period BTO/PTO superlattice. The primitive periodicity of tetragonal structure with the space group P 4mm is retained, which is more stable in energy than the rhombohedral structure. 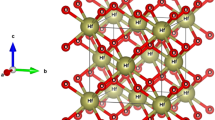For the tetragonal perovskite structure compounds BTO and PTO, the equilibrium lattice parameters are a(BTO)=3.915and, which are slightly less than the experimental values of 3.994, 4.034, 3.904 and, respectively [13, 14]. A sketch of ground state short-period BTO/PTO superlattice with its atomic positions is shown in Fig. 1.

Figure 1
figure 1

The sketch of short-period ferroelectric superlattice with its atomic positions

Full size image

To calculate the uniaxial tensile stress σ33, we apply a small strain increment η3 along the c axis and then conduct structural optimization for the lattice vectors perpendicular to the c axis, and all the internal atomic positions until the two components of stress tensor (i.e., σ11 and σ22) are smaller than 0.05 GPa. The strain is then increased step by step. Since, the elastic constants satisfy η3/η1≈ − (c11 + c12)/c13 under the loading of uniaxial tensile strain applied along the c axis, where the strains η i are calculated by η1 = η2 = (a − a0)/a0 and η3 = (c − c0)/c0, withandbeing the lattice constants of the unstrained superlattice structure. We have examined the accuracy of our calculations by studying the influence of different strains on the properties of BTO and PTO, respectively [12–15].

Results and Discussion

Figure 2a shows the uniaxial tensile stress σ33 as a function of strain η3. The relation between strains η1 and η3 is shown in the inset, which satisfy η3 > −2η1. The stress σ33 increases until reaching its maximum value of 6.85 GPa with increasing strain, indicating that the calculated ideal tensile strength is 6.85 GPa for the superlattice, which is the maximum stress required to break the superlattice. Figure 2b shows the elastic constants as a function of stress σ33, which reflect the relation between stress and strain. What is the most unexpected is that the constant c33 first decreases until reaching its minimum value at σ c = 3.26 GPa and then gradually increases, promising a large electromechanical response at σ c [27]. The minimum c33 corresponds to the minimum slope of the curve of Fig. 2a at σ c . Other elastic constants, especially c11, always decrease with increasing σ33, indicating that the superlattice under the loading of uniaxial tensile stress along the c axis becomes soft along the nonpolar axes.

Figure 2
figure 2

a Uniaxial tensile stress as a function of tensile strain η3, and the inset reflects the relation between strains η3 and η1. b Elastic constants as a function of stress σ33

Full size image

To illustrate the change of chemical bonds with uniaxial tensile stress, Fig. 3a and 3b are plotted to show the valence charge density along the c axis in the (100) and (200) planes of the superlattice at equilibrium, maximum piezoelectric coefficient and ideal tensile strength, respectively. The Pb − O4, Ba − O1, Ti1-O1 and Ti2-O4 bond lengths are not sensitive to the uniaxial tensile stress along the c axis, suggesting that the orbital hybridizations between these atoms are not sensitive to the uniaxial strain, whereas the Ti1-O3 and Ti2-O6 bonds elongate remarkably with increasing stress. Following the evolution of the charge density, we find that the weak Ti1-O3 bond starts to break first, followed by the Ti2-O6 bond. After the bond breaks, the system converts into a planar structure with alternating layers. On the other hand, Fig. 3a and 3b show that the valence charge density becomes more and more unsymmetrical with the uniaxial tensile stress increasing, indicating the increase in polarization. To confirm this, we have directly calculated the relations between the polarization and the uniaxial tensile stress with the Berry-phase approach.

Figure 3
figure 3

Calculated valence charge density along the c axis in the (100) (a) and (200) (b) planes of superlattice at equilibrium (1), maximum piezoelectric coefficient (2) and ideal tensile strength (3)

Full size image

Figure 4a shows the polarization as a function of uniaxial tensile stress. For the ground state superlattice, the calculated spontaneous polarization of 0.29 C/m2 is less than the theoretical value of 0.81 C/m2 of ground state PTO, but slightly larger than the value of 0.28 C/m2 of tetragonal BTO (the other theoretical value is 0.26 C/m2[28]), which supports the conclusion that the sharp interfaces suppress the polarization in short-period BTO/PTO superlattices [28]. As the stress σ33 increases, the polarization dramatically increases with the maximum slope appearing at σ c , indicating that the ferroelectric phase becomes more and more stable with respect to the paraelectric phase. Figure 4b shows the variation of piezoelectric coefficients with stress σ33, which are calculated by the linear response theory. The piezoelectric coefficients all increase with increasing σ33 and reach their maximum values at σ c , indicating that the appropriately applied uniaxial tensile stress can enhance the piezoelectricity for the superlattice. The piezoelectric coefficient d33 of ground state superlattice is 86.36 pC/N, which is slightly less than the value of 103.18 pC/N of PTO, but much larger than the value of 36.43 pC/N of BTO. Under the loading of uniaxial tensile stress applied along the c axis, d33 is increased from its ground state value by a factor of about 8, reaching 678.42 pC/N for the superlattice. From previous calculations [14], we know that the uniaxial tensile stress can only enhance d33 of PTO to the maximum value of 380.50 pC/N. The enhancement of piezoelectricity is supported by the conclusion of uniaxial tensile stress dependency of elastic constant c33 (see Fig. 2b). Note that the polarization under uniaxial stress remains along the <001> direction and that the piezoelectric coefficients reflect the slope of polarization versus stress curves. The enhancement of piezoelectricity corresponds to the maximum slope of the curve of Fig. 4a at σ c , it is the change of magnitude of polarization that leads to the enhancement of piezoelectricity.

Figure 4
figure 4

Uniaxial tensile stress dependence of a polarization and b piezoelectric coefficients (i.e.,d31 and d33)

Full size image

To reveal the underlying mechanisms for the abnormal piezoelectricity, we study the effects of uniaxial tensile stress on the Born effective charges and atomic displacements, respectively (see Fig. 5a, 5b). Since the atomic displacements and polarization are all along the c axis, only charges Zzz* contribute to the polarization. The uniaxial tensile stress reduces the effective charges, which remain almost constant when σ33 > σ c . The charges Zzz* of O1 and O4 atoms are much close to their normal charges, so does the case of Ti atoms when σ33 > σ c , whereas Zzz* of O3 and O6 atoms are anomalously large compared with their normal charges, suggesting the strong orbital hybridization between Ti1(and Ti2) 3d and O6(and O3) 2p states (see Fig. 3b). Note that the Ba atom is fixed at (0, 0, 0) during the first-principles simulations. The displacements of O atoms, which are much larger than those of Pb and Ti atoms for a broad range of stress, are greatly enhanced as the stress σ33 increases, especially near σ c , leading to the drastic increase in polarization. It is concluded that as the stress σ33 increases, the atomic displacements are so greatly enhanced that the overall effect is the increase in polarization, even though the magnitudes of Zzz* decrease with the stress increasing.

Figure 5
figure 5

a Born effective charges Zzz* and b atomic displacements along the c axis (in c units), relative to the centrosymmetric reference structure, as a function of uniaxial tensile stress

Full size image

Summary

In summary, we have studied the influence of uniaxial tensile stress applied along the c axis on the mechanical and piezoelectric properties of short-period BTO/PTO superlattice using first-principles methods. We show that the calculated ideal tensile strength is 6.850 GPa and that the superlattice under the loading of uniaxial tensile stress becomes soft along the nonpolar axes. We also find that the appropriately applied uniaxial tensile stress can significantly enhance the piezoelectricity for the superlattice. Our calculated results reveal that it is the drastic increase in atomic displacements along the c axis that leads to the increase in polarization and that the enhancement of piezoelectricity is attributed to the change in the magnitude of polarization with the stress. Our work suggests a way of enhancing the piezoelectric properties of the superlattices, which would be helpful to enhance the performance of the piezoelectric devices.