Abstract
Using first-principles calculations, we investigate the geometric structures and electronic properties of porous silicene and germanene nanosheets, which are the Si and Ge analogues of α−graphyne (referred to as silicyne and germanyne). It is found that the elemental silicyne and germanyne sheets are energetically unfavourable. However, after the C-substitution, the hybrid graphyne-like sheets (c-silicyne/c-germanyne) possess robust energetic and dynamical stabilities. Different from silicene and germanene, c-silicyne is a flat sheet, and c-germanyne is buckled with a distinct half-hilled conformation. Such asymmetric buckling structure causes the semiconducting behaviour into c-germanyne. While in c-silicyne, the semimetallic Dirac-like property is kept at the nonmagnetic state, but a spontaneous antiferromagnetism produces the massive Dirac fermions and opens a sizeable gap between Dirac cones. A tensile strain can further enhance the antiferromagnetism, which also linearly modulates the gap value without altering the direct-bandgap feature. Through strain engineering, c-silicyne can form a type-II band alignment with the MoS 2 sheet. The combined c-silicyne/MoS 2 nanostructure has a high power conversion efficiency beyond 20% for photovoltaic solar cells, enabling a fascinating utilization in the fields of solar energy and nano-devices.
Similar content being viewed by others
Background
Since the discovery of graphene, two-dimensional (2D) carbon nanostructures, due to their superior physical properties, have attracted substantial concerns from the fields of nano-sciences and nano-materials [1-3]. As a 2D carbon nanosheet, graphene is made of s p 2-hybridized C atoms that are regularly arranged in a honeycomb lattice. The p z orbitals of C atoms are half-filled in graphene, which results in the Dirac-like electronic structure with a semimetallic feature [2,4]. Derived from graphene, several 2D carbon allotropes have been proposed [5]. Among them, a porous carbon sheet called graphyne, which is made of both s p 2- and sp-hybridized C atoms, becomes a rising star on the horizon of graphene-related studies [6,7]. In the graphyne sheet, sp-hybridized C atoms form acetylene bonds to link the s p 2-hybridized ones. Depending on the ratio of sp constitute, graphyne can be generally classified into the α, β and γ types [8]. In the α type, each acetylene bond links one s p 2-hybridized C atom, while in the β and γ types, it links a pair and a hexagon of s p 2-hybridized C atoms, respectively [8-11]. The α type (α-graphyne) is a representative system for graphyne, which keeps the same hexagonal symmetry as graphene [12-16]. Alpha-graphyne can be regarded as an amplified graphene by inserting additional acetylene bonds into the place of C-C bonds. The semimetallic behaviour is still presented in the sheet [12-15], and the corresponding one-dimensional graphyne nanoribbons also possess similar electronic properties to the graphene ones [15,16]. Besides these common types of graphyne, theoretical studies also predict the existence of other possible structures, such as graphdiyne [17,18], 6,6,12-graphyne [10,19], δ-graphyne [20] and so on. In the experiments, graphdiyne and γ−graphyne have been synthesized through the metal-catalyzed cross-coupling reaction [21,22]. The graphdiyne-based nanotubes and nanowires have also been fabricated by the special templated synthesis method [23,24]. Experimenters further find the doping of graphdiyne benefits the photoconversion processes, which raises the power conversion efficiency of solar cells [25,26].
Very recently, silicene and germanene nanosheets, which are the Si and Ge counterparts of graphene, have been produced in the experiments [27,28]. Different from graphene, the basal planes of silicene and germanene are buckled with a chair-like buckled conformation [29]. The Dirac-like electronic structures are still present in these buckled sheets [30]. A lots of investigations have been performed on silicene and germanene [31-45], which are found to possess several peculiar characteristics, such as electric-field/substrate-induced gaps [31-35], strain-induced self-dopings [36-39], high-efficient thermoelectric performances [40-42], and promising applications for Li batteries [43-45]. However, so far, the information about the porous silicene and germanene, especially the graphyne-like Si and Ge ones (which we refer to as silicyne and germanyne thereafter), is still unknown. What are favourable structures for these porous sheets? How about their stability comparing to other 2D Si/Ge nanosheets? Do they possess particular electronic properties? To address these issues, we perform a comprehensive first-principles investigation on silicyne and germanyne, for which the unusual atomic structures and electronic properties are revealed in detail.
Methods
The first-principles calculations are performed by the VASP code with projector augmented wave pseudopotentials and plane-wave basis sets [46,47]. The cutoff energy of plane-wave basis is set to 500 eV, and a vacuum layer up to 15 Å is utilized to simulate the isolated 2D sheet. The Monkhorst-Pack scheme is adopted to sample the Brillouin zone, which uses a 9×9×1 and 15×15×1k-mesh in the relaxed and static calculations, respectively. During the structural relaxation, the Perdew-BurkeErnzerhof (PBE) exchange and correlation (XC) functional are used. All the lattice constants as well as atomic coordinates are fully optimized until the convergence of force on each atom is less than 0.01 eV/Å. The hybrid XC functional of Heyd-Scuseria-Ernzerhof (HSE) is also used in the band structure calculations, which adopts the HSE06 form with a screening parameter of 0.11 bohr −1 [48]. In view of the large computing resources required for the hybrid functional, HSE calculations are performed by the FHI-aims code with a numeric local orbital basis set [49]. We find that the two codes give consistent results despite of the basis set difference. The dynamical stabilities of nanosheets are studied by the Phonopy code [50], which is performed on a supercell with 4×4 units.
Results and discussion
Structural stability
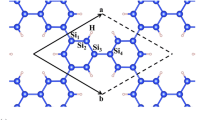
Firstly, the elemental silicyne sheet is investigated. After full structural optimization, the Si atoms are buckled in silicyne as shown in Figure 1a. In this buckled structure, the twofold-coordinated Si atoms have a higher buckling height than the threefold-coordinated ones. The cohesive energy (E coh), defined as the difference between the energy of compound and the sum of the corresponding isolated atomic energies, is −3.11 eV per atom for silicyne. As listed in Table 1, this value is larger than that of silicene (−3.95 eV) and much higher than the graphyne value (−7.03 eV), suggesting the weaker stability of elemental silicyne. Figure 1b depicts the phonon dispersion of silicyne, which shows an amount of negative frequencies in the reciprocal space. This indicates the elemental silicyne sheet is dynamically unstable, which can not sustain the free-standing state. By analysing the partial density of phonon states, we find the negative frequencies are predominantly related to the twofold-coordinated Si atoms in the porous sheet. Thus, in order to obtain a stable structure, acetylene bonds are needed to replace the twofold-coordinated Si ones.
The C-substituted silicyne (c-silicyne) can be formed by inserting −C≡C− (acetylene part) into the place of Si-Si bonds of silicene sheet, as shown in Figure 1c. In the calculations, a buckled sheet is initially set for c-silicyne, but the optimized structure becomes a flat plane akin to graphyne. The C-C distance in c-silicyne is 1.24 Å, which is a typical value for the C-C triple bond. The Si-C distance is 1.76 Å, also close to the Si-C bond length in a hexagonal SiC sheet. As shown in Table 1, the cohesive energy of c-silicyne is −6.09 eV, which is about 3 eV smaller than that of elemental silicyne and even lower than that of the SiC sheet (−5.97 eV). Comparing to graphyne (−7.03 eV), the discrepancy in the cohesive energy stems from the bond difference between c-silicyne and graphyne. In the primitive cell of c-silicyne, it contains six Si-C bonds and three C ≡C bonds, while in graphyne the C-C bonds replace the Si-C ones. The energy difference between C-C and Si-C bonds (Δ E CC−SiC) can be evaluated from the cohesive energy difference between graphene and SiC sheets, which is 3/2Δ E CC−SiC=E coh(graphene)−E coh(SiC)=−1.98 eV. Based on this bond difference, the discrepancy of cohesive energy between graphyne and c-silicyne would be E coh(graphyne)−E coh(c−silicyne)=3/4Δ E CC−SiC=−0.99 eV, which agrees well with the first-principles result of −0.94 eV. Thus, owing to the C-substitution, the weaker Si-Si and Si ≡Si bonds are replaced by the Si-C and C ≡C ones, which greatly enhances the energetic stability of silicyne. Moreover, the phonon calculations in Figure 1d show that the c-silicyne sheet has no soft modes as a dynamically stable system. The good energetic and dynamical stabilities imply that the c-silicyne could be possibly synthesized experimentally. It is found that the acetylene part in c-silicyne induces high frequencies around the 2,000 cm −1. These modes are from the stretching vibration of C ≡C bonds, which would be a Raman signature for the finding of c-silicyne [51,52].
For the germanyne, similar to the Si case, the elemental sheet has a large cohesive energy of −2.60 eV, which is higher than that of hexagonal germanene (−3.24 eV). The cohesive energy could be markedly reduced by the C-substitution, which becomes −5.52 eV for the c-germanyne with a flat conformation. This value is even lower than the GeC sheet as listed in Table 1. However, the flat conformation is dynamically unstable with a negative frequency about −150 cm −1 in the reciprocal space as shown in Figure 2a. It suggests that a spontaneous buckle would arise in c-germanyne. To this end, a chair conformation is checked firstly, in which one Ge atom is upward and the other one is downward as shown in Figure 2b. After optimization, the chair conformation is 157 meV/unit lower than the flat one, but it is still dynamically unstable with a negative frequency of −136 cm −1 at the Γ point. Then, a hilled-buckling structure is considered, for which the two Ge atoms in the unit cell are both upward as shown in Figure 2c. It is found that the hilled conformation is 16 meV/unit lower than the chair one and the soft mode is also weakened, whose negative frequency is reduced to −78 cm −1. Finally, a half-hilled conformation is studied. As depicted in Figure 2d,e,f, in the unit cell, one Ge atom is upward while the other one locates in the same plane with neighbouring C atoms. The buckling height of the upshifted Ge atom (Ge u ) is 0.94 Å, which pulls the three adjacent C atoms (C au) out of plane by about 0.12 Å. Such half-hilled conformation is dynamically stable with no soft modes as shown in Figure 2d. Furthermore, it has the lowest total energy for c-germanyne, which is 112, 128 and 235 meV/unit lower than the hilled, chair and flat ones, respectively. With the half-hilled conformation, the c-germanyne has a cohesive energy of −5.55 eV, which is 1.48 eV higher than the graphyne value due to the energy difference between Ge-C and C-C bonds. However, compared to the hexagonal germanene sheet (−3.24 eV), the c-germanyne has a stronger energetic stability, and thus, it is also much possible to be fabricated in the experiment. Figure 3 depicts the simulated Raman and infrared (IR) spectra of c-silicyne and c-germanyne by the PHonon of PWscf code [53]. It can be seen that a remarkable Raman peak is at about 2,000 cm −1 for both sheets. This Raman signature is the fingerprint of graphyne-like structure [51,52], which would be also used to find the c-silicyne and c-germanyne structures. Besides that, due to the different buckling structures, the c-silicyne and c-germanyne have distinct IR spectra. The c-silicyne sheet has two noticeable IR peaks at the approximately 300 and 900 cm −1, while the c-germanyne sheet has only one remarkable IR peak at the approximately 2,000 cm −1. Thus, in the experiment, the Raman measurement can be used to identify the graphyne-like Si and Ge nanosheets, while the IR measurement can distinguish different buckling structures in them.
Electronic structures
The PBE band structures and density of states (DOSs) of c-silicyne are depicted in Figure 4a,b. Akin to graphyne, c-silicyne possesses a Dirac-like electronic property, for which the bottom conduction and top valence bands touch each other at the K point, i.e. Dirac point. The linear dispersions of bands are obtained around the Dirac point as \(E(k)=\pm \hbar k v_{F}\), and the Fermi velocity v F is estimated to be 5.4×105 m/s by the PBE calculation. From the analysis of partial DOSs (PDOSs), it can be seen that the states around the Fermi level are dominated by the Si p z orbitals. The C p z orbitals also give a small contribution to these states. Some sharp δ-like peaks are evident at the −3.7, 1.2 and 2.8 eV of DOSs as shown in Figure 4b. They are in-plane bonding and antibonding states between Si-C and C-C atoms in c-silicyne, which cause the nearly dispersionless bands in Figure 4a.
For c-germanyne, its flat conformation has a similar electronic property to c-silicyne as shown in the inset of Figure 4c. However, the half-hilled conformation discards the semimetallic feature in c-germanyne, transforming it into a semiconductor as shown in Figure 4c. The valence band maximum (VBM) and conduction band minimum (CBM) are both at the K point, which causes a direct bandgap with the PBE value of 0.86 eV. Such gap opening is due to the breaking of sublattice symmetry by the half-hilled buckling in c-germanyne, whose VBM and CBM are located at different Ge atoms as shown in Figure 4e,f. The PDOSs analysis shows that the p z orbitals of Ge u atoms compose the top valence band and the Ge f p z ones contribute to the bottom conduction band. As indicated in Figure 2f, the Ge u atoms are buckled out of plane, while the Ge f ones stay in the same plane with neighbouring C atoms. The corresponding angle of ∠ C−G e−C is 104° and 120° for the Ge u and Ge f atoms, respectively. Thus, the hybridization of Ge u atom possesses evident s p 3 composition, while the Ge f one has a pure s p 2 hybridization. Since the s p 3 hybridization is more favourable than the s p 2 one for Ge element, the p z orbital of Ge u atom is occupied while the Ge f one is empty. Therefore, the asymmetric buckling results in two inequivalent Ge atoms, which causes a semiconducting behaviour into c-germanyne.
Since the conventional PBE functional would underestimate the bandgaps of semiconductors [54,55], we perform a further calculation by the hybrid HSE XC functional on c-silicyne and c-germanyne. Figure 5 depicts the HSE band structures from the non-spin-polarized calculations, which are analogous to the PBE results in Figure 4. c-Germanyne is found to be a direct-bandgap semiconductor with a sizeable gap of 1.11 eV, and for c-silicyne the semimetallic behaviour is also observed, whose Fermi velocity is increased to 6.4 ×105 m/s by HSE calculations. More interestingly, different from PBE calculations, the spin-polarized HSE calculations find that a spontaneous magnetism would appear in c-silicyne. There is a stable antiferromagnetic (AFM) state, which is 0.014 eV/unit lower than the nonmagnetic (NM) state. The distribution of spin densities for AFM state is shown in Figure 5d. The magnetism of two Si atoms is opposite, which causes a regular anti-parallel coupling between the Si-C and C-C atoms. The Mulliken charge analysis shows the Si and C atoms have a magnetic moment of 0.24 and 0.12 μ B , respectively. Previous studies have reported that the appearance of such AFM state is due to a large ratio of the onsite electron-electron Coulomb energy U to the electronic hopping integral t on the honeycomb sheet [56]. Thus, for graphene, a large tension is needed to reduce the hopping integral between C p z orbitals for the antiferromagnetism [56]. Whereas in c-silicyne, the Si p z orbitals dominate the state around the Fermi level. Due to the existence of -C ≡C- part, the distance between Si atoms is large, which causes a small hopping integral for Si p z ones. As a result, c-silicyne can possess a stable AFM state without strains. On the other hand, c-germanyne has a gap at the Fermi level, for which the zero density of states hinders the occurrence of spin-polarization. It would be noted that the antiferromagnetism causes a gap opening in c-silicyne at the K point as shown in Figure 5c. Following the relativistic dispersion relation of \(E(k)=\pm \sqrt {\hbar ^{2} k^{2}{v_{F}^{2}}+m^{2}{v_{F}^{4}}}\) for a massive Fermion [57], the opening gap is related to the Fermion mass as \(E_{g}/2=m{v_{F}^{2}}\). Thus, the antiferromagnetism produces a mass for the Dirac fermions in c-silicyne, which is estimated to be 0.15 m 0 from the HSE gap of 0.71 eV (m 0 is the mass of a free electron).
Strain engineering
The strain engineering is an effective way to tailor the properties of nanomaterials [58]. For c-silicyne and c-germanyne, we firstly investigate their elastic characteristics. The elastic moduli are calculated by the energy-vs.-strain method [59,60]. For c-silicyne, we obtain the C 11 and C 12 of 61.6 and 54.8 N/m, respectively. Accordingly, the Poisson ratio and Young modulus of c-silicyne are obtained as ν=C 12/C 11=0.89 and E=C 11−ν C 12=12.8 N/m, respectively. While for c-germanyne, its buckled structure weakens the stiffness. The C 11 and C 12 drop to 20.2 and 15.0 N/m, respectively, which causes a small value of 9.1 N/m (0.74) for the E (ν). Comparing to graphyne (C 11 = 95 and C 12 = 83 N/m [14], equal to E=22.5 N/m and ν=0.87), the c-silicyne and c-germanyne sheets are much softer, which would be more easily tailored by external strains. Then, the stress-strain relations of c-silicyne and c-germanyne are investigated by applying homogeneous tensions on the sheets. As shown in Figure 6a, the elastic limit of c-silicyne is at the 0.14 strain with a maximum stress of 7.3 N/m. However, a further check by phonon calculations shows that a soft mode begins to appear at the 0.10 strain, which leads to the in-plane phonon failure for c-silicyne. Thus, the phonon instability reduces the upper bound of strain for c-silicyne, whose critical strain and fracture stress are 0.09 and 6.3 N/m, respectively. While for c-germanyne, its elastic limit is at the 0.08 strain with a maximum stress of 3.0 N/m as shown in Figure 6b. The failure of c-germanyne is determined by the elastic instability, for which under the critical 0.08 strain the stretched sheet is still dynamically stable as shown in the inset of Figure 6b.
The stress-strain relation for c-silicyne and c-germanyne. The inset in (a) depicts the phonon curves of c-silicyne at the 0.10 strain, and the inset in (b) corresponds to the phonon curves of c-germanyne at the 0.08 strain. (c,d) The HSE gap variations of c-silicyne and c-germanyne under the tensile strains. The inset in (c) is the variation of E M for the antiferromagnetism in c-silicyne.
Under the strains, an arc-shaped variation of bandgap is found in c-germanyne. As shown in Figure 6d, the tensile strain firstly decreases the gap value, which reaches the minimum of 0.79 eV at the 0.03 strain. Then, the bandgap rises with the increasing strain. It gets to the maximum of 1.52 eV at the critical 0.08 strain. Such non-monotonic variation is attributed to two competitive factors of bandgap in c-germanyne. One is the buckling effect in the structure, which helps the opening of bandgap. While the other is the localization effect induced by strains, which lowers the orbital overlapping. Consequently, the band widths are narrowed and the corresponding bandgap is broadened by the localization effect. Under the strains, the buckles of Ge atoms are weakened, which causes the decrease of bandgap under a small tension. When the strain is increasing, the localization effect becomes more pronounced under the large tension, which increases the bandgap. Thus, the strain-modulated c-germanyne possesses an arc-shaped variation for the bandgap.
For c-silicyne, its NM state is always a semimetal under the strains, similar to the graphene case [61]. While for AFM state, the stability of antiferromagnetism is enhanced under the tensions. The strain-induced localization effect reduces the electronic hopping integral t, which leads to a larger value U/t and avails to a stronger antiferromagnetism. As shown in the inset of Figure 6c, at the 0.02 strain, the magnetic energy (E M =E AFM−E NM) of c-silicyne is increased to 0.026 eV/unit, which is approximately the energy of thermal fluctuation at room temperature (E T ∼k B T=0.0258 eV). When the strain grows up to 0.08 to 0.09, the E M is even larger than 0.1 eV. It indicates that the AFM state has a robust stability in these strained sheets. Accompanied with the strengthening of AFM state, the bandgap of c-silicyne is also raised. Since the opening gap is dependent on the antiferromagnetism, a monotonic increasing of bandgap is obtained as shown in Figure 6c. The linear relationship exists between the bandgap and tensile strain, and the slope corresponds to a bandgap-deformation potential of 4.39 eV/Å for c-silicyne. At the 0.09 strain, the gap value of c-silicyne can get to 1.46 eV without altering the direct-bandgap feature, suggesting the promising applications for solar energy.
Solar cell applications
The well controllable direct bandgap enables potential solar cell applications for c-silicyne. As a competitive candidate, it requires that c-silicyne has (i) a strong adsorption ability for the visible light and (ii) a suitable band alignment with acceptor materials for the electron-hole separation. To investigate this feasibility, the linear absorption of light is calculated by the HSE XC functional. As shown in Figure 7b, at the strain-free state, due to the interband VBM-CBM transition, a prominent adsorption peak starts from the bandgap of c-silicyne at 0.71 eV. It exhibits a strong adsorption ability up to 3.5 eV. Under tensile strains, the adsorption peak is red-shifted, but it still covers the whole visible-light region of [1.61, 3.10] eV. Thus, c-silicyne meets the first requirement for solar cell applications. Then, the absolute energies of CBM and VBM in c-silicyne are calculated as −4.32 and −5.03 eV, respectively. We find this CBM value is close to that of the MoS 2 nanosheet, which is −4.22 eV by the same HSE calculations, while the VBM of c-silicyne is much higher than the MoS 2 value of −6.38 eV. Under the strains, the CBM of c-silicyne moves upwards slowly and it can exceed the MoS 2 value at the 0.06 strain. The VBM of c-silicyne is down-shifted, but it is always above the VBM of MoS 2 sheet as shown in Figure 7c. Thus, starting from the 0.06 strain, a type-II band alignment can be formed between the MoS 2 and c-silicyne sheets, which satisfies the second requirement for high-efficiency solar cells. For c-germanyne, we find that its CBM/VBM is −4.53/−5.64 eV and the strain-induced variation is arc-shaped. Hence, it is hard to find an appropriate common acceptor material for it, which limits the solar energy application of c-germanyne.
Optical adsorption, band alignment and power-conversion efficiency. (a) The optical adsorption of c-silicyne at the ε=0 and 0.09 strains. (b) The band alignment between MoS 2 and strained c-silicyne sheets. (c) Calculated power-conversion efficiency as a function of the donor bandgap and conduction band offset, in which the values of c-silicyne/MoS 2 system are marked as stars.
When c-silicyne is superimposed with a MoS 2 sheet, the power conversion efficiency (PCE) η for this c-silicyne/MoS 2 heterostructure can be theoretically estimated in the limit of 100% external quantum efficiency as [62-66]:
Here, the band-fill factor (β FF) is adopted to 0.65, the open-circuit voltage (V oc) is set to \({E_{g}^{d}}-\Delta E_{c}-0.3\), where \({E_{g}^{d}}\) is the bandgap of donor, Δ E c is the conduction band offset between the acceptor and donor, and 0.3 is an empirical factor for energy conversion kinetics [66,67]. The integral in the numerator is the short circuit current J sc calculated in a limit external quantum efficiency of 100% [67,68], and the denominator is the integrated AM 1.5 solar energy flux, which amounts to 1,000 W/m 2 [62-66]. We find that under the strains of 0.06 to 0.09, the η of c-silicyne/MoS 2 heterostructure can exceed 20% as shown in Figure 7d. When a 0.06 strain is applied to c-silicyne, the power conversion efficiency η reaches the maximum value of 23.1%. Under larger strains of 0.7 to 0.9, η becomes 22.5%, 22.4% and 21.4%, respectively. These high power conversion efficiencies are comparable to those of recent proposed phosphorene and graphene-like Si-C nanostructures [62-65]. Therefore, the c-silicyne sheet would be a fascinating nanomaterial for solar energy applications, especially in thin-film photovoltaic systems.
Finally, we briefly discuss the possible synthesis approach for c-silicyne. Benefited from the recent development of metal-assisted coupling methods, several porous nanostructures have been successfully fabricated by self-assembling the molecular building blocks [21,22,69]. Through changing different molecular precursors and metal substrates, the experimenters can design the morphology of novel porous nanosheets and manufacture the well-defined nanostructures [70-74]. It seems the ethynyl(methylene)silyl [75], which contains both Si-C and Si-C ≡C parts in its molecular structure, will be a possible molecular building block for silicyne. After choosing a suitable metal surface as substrates, the metal-catalyzed cross-coupling reaction, which has been used in the synthesis of graphyne [21,22], would be also valid to fabricate the silicyne sheet.
Conclusions
In summary, we have systematically investigated the structures and properties of porous silicene and germanene nanosheets, i.e. silicyne and germanyne ones. We find that the C-substitution could significantly enhance the energetic and dynamical stabilities of these systems. Different from silicene, the c-silicyne sheet prefers a flat plane, while the c-germanyne favors a unique half-hilled buckled conformation. Such half-hilled conformation brings a semiconducting behaviour into c-germanyne, which is distinct from the graphyne and germanene nanosheets. For c-silicyne, it exhibits a zero-bandgap semimetallic behaviour at the nonmagentic state but becomes a direct-bandgap semiconductor at the antiferromagnetic state. Under tensile strains, the antiferromagnetism in c-silicyne could be strengthened and the bandgap is also linearly raised. More interestingly, when the strained c-silicyne sheet is superimposed onto a MoS 2 monolayer, the heterostructure can be a promising solar-cell material with high power conversion efficiencies exceeding 20%. Our studies demonstrate that the silicyne and germanyne nanosheets possess peculiar electronic and magnetic properties, which have potential applications in the fields of solar energy and nano-devices.
References
Geim AK, Novoselov KS. The rise of graphene. Nat Mater. 2007; 6(3):183–91.
Avouris P, Dimitrakopoulos C. Graphene: synthesis and applications. Mater Today. 2012; 15(3):86–97.
Tang Q, Zhou Z. Graphene-analogous low-dimensional materials. Prog Mater Sci. 2013; 58(8):1244–315.
Allen MJ, Tung VC, Kaner RB. Honeycomb carbon: a review of graphene. Chem Rev. 2009; 110(1):132–45.
Peng Q, Dearden AK, Crean J, Han L, Liu S, Wen X, et al.New materials graphyne, graphdiyne, graphone, and graphane: review of properties, synthesis, and application in nanotechnology. Nanotechnol Sci Appl. 2014; 7:1–29.
Ivanovskii AL. Graphynes and graphdyines. Prog Solid State Chem. 2013; 41:1–19.
Li Y, Xu L, Liu H, Li Y. Graphdiyne and draphyne: from theoretical predictions to practical construction. Chem Soc Rev. 2014; 43:2572–86.
Kim BG, Choi HJ. Graphyne: Hexagonal network of carbon with versatile dirac cones. Phys Rev B. 2012; 86:115435.
Zhang Y, Pei Q, Wang C. Mechanical properties of graphynes under tension: a molecular dynamics study. Appl Phys Lett. 2012; 101(8):081909.
Chen J, Xi J, Wang D, Shuai Z. Carrier mobility in graphyne should be even larger than that in graphene: a theoretical prediction. J Phys Chem Lett. 2013; 4(9):1443–48.
Padilha JE, Fazzio A, da Silva AJR. Directional control of the electronic and transport properties of graphynes. J Phys Chem C. 2014; 118(32):18793–8.
Leenaerts O, Partoens B, Peeters F. Tunable double dirac cone spectrum in bilayer α-graphyne. Appl Phys Lett. 2013; 103(1):013105.
Ozcelik VO, Ciraci S. Size dependence in the stabilities and electronic properties of α-graphyne and its boron nitride analogue. J Phys Chem C. 2013; 117(5):2175–82.
Ducere J-M, Lepetit C, Chauvin R. Carbo-graphite: structural, mechanical, and electronic properties. J Phys Chem C. 2013; 117(42):21671–81.
Yue Q, Chang S, Kang J, Tan J, Qin S, Li J. Magnetic and electronic properties of α-graphyne nanoribbons. J Chem Phys. 2012; 136(24):244702.
Yue Q, Chang S, Tan J, Qin S, Kang J, Li J. Symmetry-dependent transport properties and bipolar spin filtering in zigzag α-graphyne nanoribbons. Phys Rev B. 2012; 86:235448.
Long M, Tang L, Wang D, Li Y, Shuai Z. Electronic structure and carrier mobility in graphdiyne sheet and nanoribbons: theoretical predictions. ACS Nano. 2011; 5(4):2593–600.
Niu X, Mao X, Yang D, Zhang Z, Si M, Xue D. Dirac cone in α-graphdiyne: a first-principles study. Nano Res Lett. 2013; 8(1):469.
Malko D, Neiss C, Viñes F, Görling A. Competition for graphene: graphynes with direction-dependent dirac cones. Phys Rev Lett. 2012; 108:086804.
Zhao M, Dong W, Wang A. Two-dimensional carbon topological insulators superior to graphene. Sci Rep. 2013; 3:3532.
Li G, Li Y, Liu H, Guo Y, Li Y, Zhu D.Architecture of graphdiyne nanoscale films. Chem Commun. 2010; 46(19):3256–8.
Tahara K, Yamamoto Y, Gross DE, Kozuma H, Arikuma Y, Ohta K, et al. Syntheses and properties of graphyne fragments: trigonally expanded dehydrobenzo[12]annulenes. Chem Eur J. 2013; 19(34):11251–60.
Li G, Li Y, Qian X, Liu H, Lin H, Chen N, et al.Construction of tubular molecule aggregations of graphdiyne for highly efficient field emission. J Phys Chem C. 2011; 115(6):2611–5.
Qian X, Ning Z, Li Y, Liu H, Ouyang C, Chen Q, et al. Construction of graphdiyne nanowires with high-conductivity and mobility. Dalton Trans. 2012; 41(3):730–33.
Du H, Deng Z, Lv Z, Yin Y, Yu L, Wu H, et al. The effect of graphdiyne doping on the performance of polymer solar cells. Synth Met. 2011; 161(19):2055–7.
Tang H, Hessel CM, Wang J, Yang N, Yu R, Zhao H, et al. Two-dimensional carbon leading to new photoconversion processes. Chem Soc Rev. 2014; 43(13):4281–99.
Vogt P, De Padova P, Quaresima C, Avila J, Frantzeskakis E, Asensio MC, et al. Silicene: compelling experimental evidence for graphenelike two-dimensional silicon. Phys Rev Lett. 2012; 108(15):155501.
Daila ME, Xian L, Cahangirov S, Rubio A, Lay GL. Germanene: a novel two-dimensional germanium allotrope akin to graphene and silicene. New J Phys. 2014; 16(9):095002.
Jose D, Datta A. Structures and chemical properties of silicene: unlike graphene. Acc Chem Res. 2014; 47(2):593–602.
Roome NJ, Carey JD. Beyond graphene: Stable elemental monolayers of silicene and germanene. ACS Appl Mater Interfaces. 2014; 6(10):7743–50.
Drummond N, Zolyomi V, Fal’Ko V. Electrically tunable band gap in silicene. Phys Rev B. 2012; 85(7):075423.
Houssa M, van den Broek B, Scalise E, Pourtois G, Afanas’ ev V, Stesmans A. An electric field tunable energy band gap at silicene/(0001) ZnS interfaces. Phys Chem Chem Phys. 2013; 15(11):3702–5.
An X-T, Zhang Y-Y, Liu J-J, Li S-S. Quantum spin hall effect induced by electric field in silicene. Appl Phys Lett. 2013; 102(4):043113.
Zhu J, Schwingenschlogl U. Structural and electronic properties of silicene on MgX2 (X = CI, Br, and I). ACS Appl Mater Interfaces. 2014; 6(14):11675–81.
Li X, Wu S, Zhou S, Zhu Z. Structural and electronic properties of germanene MoS2 monolayer and silicene/MoS2 monolayer superlattices. Nano Res Lett. 2014; 9(1):110.
Kaloni T, Schwingenschlögl U. Stability of germanene under tensile strain. Chem Phys Lett. 2013; 583:137–40.
Wang Y, Ding Y. Strain-induced self-doping in silicene and germanene from first-principles. Solid State Commun. 2013; 155:6–11.
Kaloni T, Cheng Y, Schwingenschlögl U. Hole doped dirac states in silicene by biaxial tensile strain. J Appl Phys. 2013; 113(10):104305.
Qin R, Zhu W, Zhang Y, Deng X. Uniaxial strain-induced mechanical and electronic property modulation of silicene. Nano Res Lett. 2014; 9(1):521.
Zberecki K, Wierzbicki M, Barnaś J, Swirkowicz R. Thermoelectric effects in silicene nanoribbons. Phys Rev B. 2013; 88(11):115404.
Zberecki K, Swirkowicz R, Wierzbicki M, Barnaś J. Enhanced thermoelectric efficiency in ferromagnetic silicene nanoribbons terminated with hydrogen atoms. Phys Chem Chem Phys. 2014; 16:12900–08.
Yang K, Cahangirov S, Cantarero A, Rubio A, D’Agosta R. Thermoelectric properties of atomically thin silicene and germanene nanostructures. Phys Rev B. 2014; 89(12):125403.
Tritsaris GA, Kaxiras E, Meng S, Wang E. Adsorption and diffusion of lithium on layered silicon for Li-ion storage. Nano Lett. 2013; 13(5):2258–63.
Setiadi J, Arnold MD, Ford MJ. Li-ion adsorption and diffusion on two-dimensional silicon with defects: a first principles study. ACS Appl Mater Interfaces. 2013; 5(21):10690–95.
Tan X, Cabrera CR, Chen Z. Metallic BSi3 silicene: a promising high capacity anode material for lithium-ion batteries. J Phys Chem C. 2014; ASAP:10–1021503597.
Kresse G, Furthmuller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci. 1996; 6(1):15–50.
Kresse G, Furthmuller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B. 1996; 54(16):11169–86.
Brothers EN, Izmaylov AF, Normand JO, Barone V, Scuseria GE. Accurate solid-state band gaps via screened hybrid electronic structure calculations. J Chem Phys. 2008; 129(1):011102.
Blum V, Gehrke R, Hanke F, Havu P, Havu V, Ren X, et al. Ab initio molecular simulations with numeric atom-centered orbitals. Comput Phys Commun. 2009; 180(11):2175–96.
Togo A, Oba F, Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys Rev B. 2008; 78:134106.
Popov VN, Lambin P. Theoretical raman fingerprints of α-, β-, and γ-graphyne. Phys Rev B. 2013; 88:075427.
Perkgoz NK, Sevik C. Vibrational and thermodynamic properties of α-, β-, γ- and 6, 6, 12-graphyne structures. Nanotechnology. 2014; 25(18):185701.
Giannozzi P, Baroni S, Bonini N, Calandra M, Car R, Cavazzoni C, et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J Phys: Condens Matter. 2009; 21(39):395502–119.
Janesko BG, Henderson TM, Scuseria GE. Screened hybrid density functionals for solid-state chemistry and physics. Phys Chem Chem Phys. 2009; 11(3):443–54.
Barone V, Hod O, Peralta JE, Scuseria GE. Accurate prediction of the electronic properties of low-dimensional graphene derivatives using a screened hybrid density functional. Acc Chem Res. 2011; 44(4):269–79.
Lee S-H, Kim S, Kim K. Semimetal-antiferromagnetic insulator transition in graphene induced by biaxial strain. Phys Rev B. 2012; 86(15):155436.
Longuinhos R, Moujaes EA, Alexandre SS, Nunes RW. Theoretical chemistry of α-graphyne: functionalization, symmetry breaking, and generation of dirac-fermion mass. Chem Mater. 2014; 26(12):3701–08.
Li J, Shan Z, Ma E. Elastic strain engineering for unprecedented materials properties. MRS Bull. 2014; 39(02):108–14.
Cadelano E, Palla PL, Giordano S, Colombo L. Elastic properties of hydrogenated graphene. Phys Rev B. 2010; 82(23):235414.
Wang Y, Ding Y. Mechanical and electronic properties of stoichiometric silicene and germanene oxides from first-principles. Phys Status Solidi-RRL. 2013; 7(6):410–3.
Choi S-M, Jhi S-H, Son Y-W. Effects of strain on electronic properties of graphene. Phys Rev B. 2010; 81:081407.
Guo H, Lu N, Dai J, Wu X, Zeng XC. Phosphorene nanoribbons, phosphorus nanotubes and van der Waals multilayers. J Phys Chem C. 2014; 118(51):14051–9.
Dai J, Zeng XC. Bilayer phosphorene: effect of stacking order on bandgap and its potential applications in thin-film solar cells. J Phys Chem Lett. 2014; 5(7):1289–93.
Dai J, Wu X, Yang J, Zeng XC. AlxC monolayer sheets: two-dimensional networks with planar tetracoordinate carbon and potential applications as donor materials in solar cell. J Phys Chem Lett. 2014; 5:2058–65.
Zhou L-J, Zhang Y-F, Wu L-M. SiC2 siligraphene and nanotubes: novel donor materials in excitonic solar cells. Nano Lett. 2013; 13(11):5431–6.
Bernardi M, Palummo M, Grossman JC. Semiconducting monolayer materials as a tunable platform for excitonic solar cells. ACS Nano. 2012; 6(11):10082–9.
Scharber MC, Mühlbacher D, Koppe M, Denk P, Waldauf C, Heeger AJ, et al. Design rules for donors in bulk-heterojunction solar cells: towards 10% energy-conversion efficiency. Adv Mater. 2006; 18(6):789–94.
Dennler G, Scharber MC, Ameri T, Denk P, Forberich K, Waldauf C, et al. Design rules for donors in bulk-heterojunction tandem solar cells towards 15% energy-conversion efficiency. Adv Mater. 2008; 20(3):579–83.
Bieri M, Treier M, Cai J, Ait-Mansour K, Ruffieux P, Groning O, et al. Porous graphenes: two-dimensional polymer synthesis with atomic precision. Chem Commun. 2009; 45:6919–21.
Bieri M, Nguyen M-T, Groning O, Cai J, Treier M, Ait-Mansour K, et al. Two-dimensional polymer formation on surfaces: insight into the roles of precursor mobility and reactivity. J Am Chem Soc. 2010; 132(46):16669–76.
Cardenas L, Gutzler R, Lipton-Duffin J, Fu C, Brusso JL, Dinca LE, et al. Synthesis and electronic structure of a two dimensional [small pi]-conjugated polythiophene. Chem Sci. 2013; 4(8):3263–8.
Eichhorn J, Nieckarz D, Ochs O, Samanta D, Schmittel M, Szabelski PJ, et al. On-surface ullmann coupling: the influence of kinetic reaction parameters on the morphology and quality of covalent networks. ACS Nano. 2014; 8(8):7880–9.
Landers J, Cherioux F, Santis MD, Bendiab N, Lamare S, Magaud L, et al. Convergent fabrication of a nanoporous two-dimensional carbon network from an aldol condensation on metal surfaces. 2D Mater. 2014; 1(3):034005.
Sumpter BG, Liang L, Nicolai A, Meunier V. Interfacial properties and design of functional energy materials. Acc Chem Res. 2014; 47(11):3395–405.
CSID:9019624. http://www.chemspider.com/Chemical-Structure.9019624.html. Accessed 16 Jan 2015.
Acknowledgements
Some of the calculations were performed in the Shanghai Supercomputer Center of China. Authors acknowledge the support from the National Natural Science Foundation of China under Grant No. 11474081, 11104052, and 11104249.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
YD and YW conceived the idea, performed the calculations, analysed the data, and wrote the manuscript. Both authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ding, Y., Wang, Y. Unusual structural and electronic properties of porous silicene and germanene: insights from first-principles calculations. Nanoscale Res Lett 10, 13 (2015). https://doi.org/10.1186/s11671-014-0704-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s11671-014-0704-3