Abstract
Spectral, angular, and temporal distributions of fluorescence as well as specular reflection were investigated for silica-based artificial opals. Periodic arrangement of nanosized silica globules in the opal causes a specific dip in the defect-related fluorescence spectra and a peak in the reflectance spectrum. The spectral position of the dip coincides with the photonic stop band. The latter is dependent on the size of silica globules and the angle of observation. The spectral shape and intensity of defect-related fluorescence can be controlled by variation of detection angle. Fluorescence intensity increases up to two times at the edges of the spectral dip. Partial photobleaching of fluorescence was observed. Photonic origin of the observed effects is discussed.
Similar content being viewed by others
Background
Modification and enhancement of the fluorescence in photonic structures is important for development of optical sensors [1] and improvement of the fluorescence efficiency [2] and light harvesting ability in solar cells [3]. Most papers (see, for example, reviews [1,4]) deal with experimental and theoretical aspects of the fluorophores embedded in the multilayered films forming one-dimensional (1D) photonic crystals. The behavior of such structures is determined by the interference of light that leads to decreased reflectance and enhanced fluorescence at certain directions of observation. Fluorescence has increased intensity and higher degree of polarization at these angles, in comparison to the background emission. The increase of light intensity at certain directions may be explained by resonant coupling of fluorescence with the waveguiding leaky modes in the 1D structure that can result in shorter fluorescent lifetimes and higher radiative rates [5,6]. In particular, resonantly enhanced directional fluorescence with decreased lifetime was detected experimentally for a dye doped in 1D photonic crystals [5] and explained in terms of increased density of states near the photonic bandgap. Directional emission of light has also been reported for the multilayered films doped with quantum dots [7] and rare-earth ions [8].
Considerably less attention has been paid to the modification of light emission properties of fluorophores incorporated within three-dimensional (3D) photonic crystals, such as artificial opals composed of closely packed dielectric globules. Photonic stop zones in 3D structures have been already proved useful for blocking undesirable light emission [9]. In particular, this effect was used to avoid leakage of light from the dye-sensitized solar cells [3], to suppress the radiative channels [10], and in such a way to improve the Förster resonance energy transfer between the dye molecules situated inside the photonic structure [11].
In this work, we investigate the influence of photonic stop zones on the intrinsic fluorescence of 3D photonic crystal made of closely packed silica globules. Special attention is paid to the changes in the spectral shape of fluorescence as a function of the detection angle and the angular shift of photonic stop zone. It is demonstrated that the self-fluorescence of silica material can be enhanced at certain detection angles, near the spectral edges of the photonic stop zone.
Methods
Preparation of photonic crystals based on synthetic opals was carried out in several steps. First, the silica globules were prepared by the hydrolysis of alkyl orthosilicate. Second, sedimentation and close-packing of these globules from the solution was achieved by centrifugation. Finally, the precipitated samples were annealed to obtain solid samples with size of several cm. Two samples (marked as 1 and 2) of compacted silica globules of slightly different sizes were selected for the study.
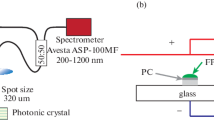
The samples were investigated by using optical and spectroscopic methods. SEM images of opals were obtained with EPMA SEI JXA-8200 microscope (JEOL Ltd., Akishima-shi, Tokyo, Japan). Reflectance spectra at the normal incidence were measured on JASCO V-570 spectrophotometer (JASCO International Co. Ltd., Tokyo, Japan), whereas the angular dependence of reflectance was acquired on a custom goniometric setup [12]. Fluorescence was excited with Nd:YAG laser emitting at 266 nm. Fluorescence spectra were detected by means of Andor SR303i spectrograph equipped with a CCD camera.
Results and discussion
The electron micrographs of the samples (Figure 1) indicate rather uniform close-packing of nanosized silica globules (on the scale of several hundred micrometers at least). The average sizes of silica globules (determined from scanning electron microscopy (SEM) images) were 276 and 230 nm for the samples 1 and 2, respectively. According to the Raman and IR spectra [13], the globules consist of amorphous silica.
Periodic spatial arrangement of silica globules results in distinct photonic properties that can be revealed in spectrally selective reflectivity. Indeed, the reflectance spectra of samples 1 and 2 (Figure 2) contain a single band of relatively strong reflectance with the peaks at 620 and 512 nm, correspondingly. The light cannot penetrate into the sample at these wavelengths, due to interference phenomena in such photonic structure.
The resonance condition depends on the direction of light propagation, and therefore, on the incidence/detection angle. The reflected light intensity was measured as a function of the detection angle for different wavelengths (Figures 3 and 4).
The incident light at 532 and 593 nm lies in the spectral range of photonic stop band for sample 1. Therefore, it is reflected stronger in the angular ranges from 35° to 55° (Figure 3a) and 15° to 35° (Figure 3b), respectively. In order to prove that the angular resonances depicted in Figure 3 will disappear outside the photonic stop band, we measured the angular dependence of light reflectance at 402 nm which is clearly outside the stop band range of the sample 1 (Figure 5). On the other hand, the wavelength 402 nm enters the stop band at the range of detection angles 50° to 70° in the case of sample 2 (Figure 4a).
In principle, one could employ the Brewster law for the estimation of effective refractive index of the samples, based on the angular dependences of reflectance, measured spectrally far from the photonic stop band (Figures 4b and 5). It was revealed, however, that the diffusely reflected light restricts this possibility.
Alternatively, the effective refractive index can be calculated using a modified Bragg law, which describes the relation between the local maximum in the reflectance spectrum λ max, the corresponding angle θ of light detection, the size of globules D, and effective refractive index n eff [14,15]:
where \( {\mathrm{a}}_{\left[111\right]}=\sqrt{\frac{2}{3}}\cdot \mathrm{D} \) is the distance between the planes of closely packed silica globules in the direction [111].
For the sample 1, we have λ 1 = 532 nm, θ 1 = 46° (Figure 3a) and λ 2 = 593 nm, θ 2 = 25° (Figure 3b). Substituting these values into the Equation 1 yields a system of two equations with two unknown parameters D and n eff. The solution of this system gives D = 276 nm and n eff = 1.38.
For the sample 2, we have λ 1 = 512 nm, θ 1 = 10° and λ 2 = 500 nm, θ 2 = 20° (Figure 6) yielding D = 230 nm and n eff = 1.38.
Obtained refractive indices correlate well with the literature data. Accurate description of optical properties of the mixed materials, particularly porous media, is not a trivial task. A list of possible approaches, by Maxwell-Garnett, Bruggeman and Lorentz-Lorenz models, Drude, or Silberstein formula, can be found in books, for example [16], and reviews [17,18]. In our knowledge, none of the approaches mentioned above is general enough to account for the shape, size, and interconnection of pores in the real sample. Also, one can use for estimation of effective refractive index an equation known as “refractive mixing model” that is mathematically described by Birchak formula (Ref. [16], page 166). This model assumes that the refractive index of a composite mixture is an average of the indices of components weighted by their corresponding volumes:
where n globule is a refractive index of silica, n inf is a refractive index of the substance contained in the pores of photonic crystal (n inf = 1 for the air), and f is the volume fraction of globules in the sample (f = 0.74 for dense hexagonal packing). Equation 2 was successfully applied earlier for the description of photonic crystals [14,15], porous films [19], and soils [20]. Effective refractive index obtained for n eff using Equation 2 was 1.39 [14] and 1.33 [15]. These values were obtained by assuming that n globule is equal to the refractive index of fused silica. In our opinion, it is a rough estimate, because silica nanoglobules are usually porous and, as a consequence, their refractive index could be slightly smaller than the refractive index of the fused silica.
Fluorescence spectra of samples excited with UV light (λ exc = 266 nm) consist of several broad, overlapping bands in the range of 400 to 700 nm (Figure 7).
Fluorescence spectra of photonic crystal samples with different spectral positions of stop zones. Numbering of spectra 1 and 2 corresponds to the numbering of samples. Spectrum 3 is fluorescence of a soda lime glass slab. Spectra 1′ and 2′ are reflectance spectra of samples 1 and 2, respectively (plotted not to scale with fluorescence).
The spectra may belong to electronic transitions in the defect centers of -Si-O-Si-O- lattice which have the energies in the visible range [21]. Particularly, the maximum at 450 nm in spectrum 2 can be associated with twofold Si-oxygen deficiency center O2 = Si: [22,23]. Fluorescence bands with maxima near 500 nm in spectra 1 and 3 can be related to the hydrogenated ≡ Si-H defects, which are formed by attaching H and OH groups to the disrupted ≡ Si• and ≡ Si-O• bonds [24]. Red luminescence in the range of 600 to 700 nm (spectra 2 and 3) can be associated with non-bridging oxygen hole centers [25] or OH groups on the surface of the silica [14].
The fluorescence emission from photonic crystals is subject to partial photobleaching. The brightness of fluorescence at the laser spot incident on the sample surface decreases essentially during the first minutes of irradiation and then changes more gradually (Figure 8). The blue fluorescence band with the maximum at 450 nm is bleaching faster than the red band with the maximum at 650 nm. As a consequence, fluorescence acquires a reddish tint at a longer exposure of the sample to UV light (Figure 8, inset).
Photobleaching of photonic crystal fluorescence in time. Unequal kinetics of blue and red fluorescence is illustrated on the example of 450 nm (1) and 650 nm (2) spectral bands excited by steady laser irradiation at 266 nm. Images of the fluorescent spot on the surface of sample 2 in the initial and bleached states are shown in the inset.
Similar photobleaching of blue fluorescence has been reported earlier for the laser-treated silica waveguides [26]. This process may be caused by photoconversion of the silica twofold deficient centers into the E′-centers initiated by the two-photon absorption [27]. Further measurements were conducted after a preliminary UV irradiation of samples in the saturation region between 800 and 1,200 s (Figure 8), where the changes of fluorescence intensity caused by photobleaching are already minimal.
Fluorescence photobleaching may be affected by light confinement inside the photonic crystal and slow non-radiative migration of excitation between the defects in SiO2 material. As a consequence, the excitation energy may decrease before reaching the defect-related fluorescence center. The longer the migration time, the smaller the energy reaching the luminescent center. Therefore, less energetic red fluorescence could become predominant after a prolonged irradiation. Similar effect and its origin have been discussed before [28].
An interesting feature in the recorded fluorescence is a dip in the spectrum 2 (Figure 7), with a minimum at 507 nm that is absent in spectra 1 and 3. This spectral feature overlaps with the maximum of reflectance, caused by photonic stop zone (Figure 7, spectrum 2′). Since the photonic stop zone of the sample 1 is almost outside the spectral range of fluorescence (Figure 7, spectrum 1′), the dip in fluorescence spectrum 1 is absent. The presence of the photonic dip in spectrum 2 demonstrates fundamental opportunity to control the spectral shape of fluorescence spectrum by 3D photonic structure of opal.
Recording fluorescence at different angles reveals a systematic shift of the abovementioned spectral dip. It shifts toward shorter wavelengths with the increase of detection angle (Figure 9). This allows to control the fluorescence intensity in the spectral range covered by the photonic stop zone by changing detection angle. The spectral position of photonic dip in the fluorescence can be described well with Equation 1.
In addition to the angular shift of the dip in fluorescence spectra, which is clearly of photonic origin, an enhancement of the fluorescence intensity was observed near the edges of spectral dip. For example, the fluorescence intensity at the detection angle of 70° is almost two times higher than that at the angle of 0° at the wavelength of 490 nm (marked by dashed line in Figure 9). We suppose that such angular enhancement in fluorescence also has photonic nature and is caused by blue shift of the photonic stop band at large angles. Similar effect was described for the light transmitted through a thin photonic crystal film [29]. The overlap of diffractional resonances associated with different systems of crystallographic planes would also lead to a redistribution of light intensity on the edges of the stop bands, which is visible for the transmitted light in Figures 2 and 3 in Ref. [29].
It should be noted that fluorescence intensity decreases at increasing of the observation angle for the fluorescent samples without a photonic superlattice, such as photonic glasses with disordered silica globules (Figure 10a) and reference slabs of soda lime glass (Figure 10b). Fluorescence emission experiences stronger refraction at high observation angles and higher reflectance at the air-glass interfaces, thus being unable to leave the sample (Figure 10a, inset).
Conclusions
We demonstrated that intrinsic fluorescence of opal-based photonic crystals can be influenced by photonic stop zone. A decrease of the fluorescence at the wavelengths within the photonic stop band and its increase near the edges of stop band were observed. This effect could be proved by comparison of the fluorescent spectra detected at different angles, despite the undesirable photobleaching of the samples.
References
Chaudhery V, George S, Lu M, Pokhriya A, Cunningham B. Nanostructured surfaces and detection instrumentation for photonic crystal enhanced fluorescence. Sensors. 2013;13:5561–84.
Ganesh N, Zhang W, Mathias P, Chow E, Soares J, Malyarchuk V, et al. Enhanced fluorescence emission from quantum dots on a photonic crystal surface. Nat Nanotech. 2007;2:515–20.
Knabe S, Soleimani N, Markvart T, Bauer G. Efficient light trapping in a fluorescence solar collector by 3D photonic crystal. Phys Status Solidi RRL. 2010;4(5–6):118–20.
Barnes W. Fluorescence near interfaces: the role of photonic mode density. J Mod Optic. 1998;45(4):661–99.
Badugu R, Nowaczyk K, Descrovi E, Lakowicz J. Radiative decay engineering 6: fluorescence on one-dimensional photonic crystals. Anal Biochem. 2013;442:83–96.
Calander N. Surface plasmon-coupled emission and Fabry-Perot resonance in the sample layer: a theoretical approach. J Phys Chem B. 2005;109:13957–63.
Sainidou R, Renger J, Teperik T, Gonzalez M, Quidant R, Javier Garcia De Abajo F. Extraordinary all-dielectric light enhancement over large volumes. Nano Lett. 2010;10:4450–5.
Dolgov L, Kiisk V, Matt R, Pikker S, Sildos I. Tailoring of the spectral-directional characteristics of rare-earth fluorescence by metal-dielectric planar structures. Appl Phys B. 2012;107:749–53.
Baert K, Kolaric B, Libaers W, Vallee R, Di Vece M, Lievens P, et al. Angular dependence of fluorescence emission from quantum dots inside a photonic crystal. Res Lett Nanotechnol. 2008;2008:4. Article ID 974072.
Krishnamoorthy H, Song J, Kretzschmar I, Menon V. Photoluminescence modification in self-assembled fluorescent 3D photonic crystals, IEEE Applications and Technology Conference (LISAT). 2010. Conference Publication:1–4.
Kolaric B, Baert K, Van der Auweraer M, Valee R, Clays K. Controlling the fluorescence resonant energy transfer by photonic crystal band gap engineering. Chem Mater. 2007;19:5547–555.
Loot A, Dolgov L, Pikker S, Lõhmus R. Goniometric setup for plasmonic measurements and characterization of optical coatings. In: Fesenko O, Yatsenko L, Brodin M, editors. Springer proceedings in physics 146: nanomaterials imaging techniques, surface studies, and applications. New York: Springer; 2013. p. 119–34.
Dovbeshko G, Fesenko O, Boyko V, Romanyuk V, Moiseyenko V, Gorelik V, et al. Vibrational spectra of opal-based photonic crystals. IOP Conf Ser Mater Sci Eng. 2012;38(1):12008–13.
Gruzintsev A, Emelchenko G, Masalov V, Romanelli M, Barthou C, Benalloul P, et al. Luminescent properties of synthetic opal. Inorg Mater. 2008;44(2):159–64.
Reynolds A, Lopez-Tejeira F, Cassagne D, Garcıa-Vidal F, Jouanin C, Sanchez-Dehesa J. Spectral properties of opal-based photonic crystals having a SiO2 matrix. Phys Rev B. 1999;60(16):11422–6.
Sihvola A. Electromagnetic mixing formulas and applications. IEE Electromagnetic Waves Series 47. London: The Institution of Electrical Engineers; 1999.
Braun M, Pilon L. Effective optical properties of non-absorbing nanoporous thin films. Thin Solid Films. 2006;496:505–14.
Hutchinson N, Coquil T, Navid A, Pilon L. Effective optical properties of highly ordered mesoporous thin films. Thin Solid Films. 2010;518:2141–6.
Taylor D, Fleig P, Hietala S. Technique for characterization of thin film porosity. Thin Solid Films. 1998;332:257–61.
Mironov V, Dobson M, Kaupp V, Komarov S, Kleshchenko V. Generalized refractive mixing dielectric model for moist soils. IEEE Trans Geosci Rem Sens. 2004;42(4):773–85.
Salh R. Defect related luminescence in silicon dioxide network: a review. In: Basu S, editor. Crystalline Silicon: Properties and Uses. Rijeka: InTech; 2011. p. 135–72.
Skuja L, Streletsky A, Pakovich A. A new intrinsic defect in amorphous SiO2: twofold coordinated silicon. Solid State Commun. 1984;50(12):1069–72.
Skuja L. Isoelectronic series of twofold coordinated Si, Ge, and Sn atoms in glassy SiO2: a luminescence study. J Non Cryst Solids. 1992;149:77–95.
Glinka Y, Lin S, Chen Y. The photoluminescence from hydrogen-related species in composites of SiO2 nanoparticles. Appl Phys Lett. 1999;75(6):778–80.
Skuja L. Optical properties of defects in silica. In: Pacchioni G, Skuja L, Griscom DL, editors. Defects in SiO2 and related dielectrics: science and technology. NATO Science Series. Netherlands: Springer; 2000. p. 73–116.
Albert J, Malo B, Johnson D, Hill K. Some optical properties of waveguides made by high energy ion implantation in fused silica, Conference Paper: Integrated Photonics Research New Orleans, Louisiana. 1992. ISBN: 1-55752-232-4
Imai H, Arai K, Imagawa H, Hosono H, Abe Y. Two types of oxygen-deficient centers in synthetic silica glass. Phys Rev B. 1988;38(17):2772–1275.
Goushcha A, Manzo A, Scott G, Christophorov L, Knox P, Barabash Y, et al. Self-regulation phenomena applied to bacterial reaction centers. 2. Nonequilibrium adiabatic potential: dark and light conformations revisited. Biophys J. 2003;84(2):1146–60.
Romanov S. Anisotropy of light propagation in thin opal films. Phys Solid State. 2007;49(3):536–46.
Acknowledgements
This work was supported by the Marie Curie ILSES project no. 612620, Russian-Ukrainian project 27-02-14, NATO SPS project NUKR.SFPP984702, Nanotwinning FP7 project (ID 294952), and European Regional Development Fund project TK114 and RFBR project 14-02-90406.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
VB and LD developed the idea of the work and were responsible for its realization. VG carried out the preparation and the necessary microscopic measurements of samples. VB, VK, and LD made the angular measurements of fluorescence. AL realized measurements of light reflection from the samples. GD, IS, and VG participated in the joint discussions with co-authors, explaining the scientific results. All authors have read and approved the final manuscript.
Authors’ information
GD has a degree of Doctor of Sciences in Solid State Physics and Biophysics and became a Professor in 2012. She is a head of Physics of the Biological Systems Department of the Institute of Physics of the National Academy of Sciences of Ukraine. Her scientific areas of interest are biophysics, nucleic acids, solid state physics, surfaces of solids, plasmonics, surface enhancement spectroscopy, the Langmuir-Blodgett technique, AFM microscopy, and computational chemistry). She is (co)-author of more than 250 scientific publications.
VB has finished his PhD thesis titled “Optical properties of synthetic opals infiltrated by biomolecules”. His scientific areas of interest are optics, nonlinear optics, photonic crystals, solid state physics, luminescence enhancement, biophysics, and nucleic acids. He was involved in the study of optical properties (Bragg reflection, luminescence, and Raman and IR spectroscopy) of photonic crystals based on synthetic opal containing biological molecules and cells infiltrated in porous of photonic crystal.
VG has a degree of Doctor of Sciences in Optics and has received a Professor degree in 1990. He is a head of Raman Scattering Laboratory of the Lebedev Physical Institute of the Russian Academy of Sciences in Moscow. His scientific areas of interest are photonic crystals, Raman scattering, and spectroscopy of biological substances. He has investigated Raman and fluorescence spectra of a number of molecular and solid state systems, incorporated into photonic crystal pores, and has observed secondary emission enhancement at certain conditions. He has more than 300 publications in international scientific journals.
VK, PhD, is a senior scientist at the Institute of Physics, University of Tartu. He is qualified in experimental optical spectroscopy of solid state materials, with the main interests in rare earth activated, or intrinsically luminescent inorganic matrices (especially oxides), as well as photonic applications of the respective micro- and nanostructures. He is author of 38 scientific papers in the ISI referred journals.
LD, PhD, is senior research scientist at the Institute of Physics, University of Tartu. He has experience in the optical properties of composite materials containing nanoparticles. Among his scientific interests are plasmon-polariton waves in noble metal films and localized plasmons in metal nanoparticles; plasmon-coupled fluorescence; surface-enhanced light absorption, particularly plasmon-assisted light harvesting in solar cells; surface-enhanced Raman scattering; and resonance optical phenomena in dielectric and metal-dielectric nanostructures. He is author of about 40 scientific publications in the ISI referred journals.
IS, PhD, is head of the Laser spectroscopy laboratory at the Institute of Physics, University of Tartu, a member of SPIE and Physical Society of Estonia, and a member of Italian branch of the European Optical Society. His scientific interests include optical properties of low-dimensional nanomaterials; design and study of advanced materials for applications in optical memories, light emitters, waveguiding and optical sensing; microspectroscopy of single quantum emitters (molecules, quantum dots, nanotubes); surface-enhanced fluorescence and Raman scattering of single emitters; design of cryogenic equipment; etc. He is author of more than 100 scientific publications in the ISI referred journals.
AL is a PhD student and keeps also an engineer position at the Laboratory of laser spectroscopy at the Institute of Physics, University of Tartu. He has became a co-author of three scientific publications in the ISI referred journals and one book chapter even before the starting his PhD studies. These works and his current interests are related to the plasmonic and photonic properties of dielectric and metal-dielectric nanostructures. AL’s Master thesis titled “Characterization of surface plasmons on thin gold film in Kretschmann configuration” prepared under the supervision by LD was honored with Estonian National award for student works.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Boiko, V., Dovbeshko, G., Dolgov, L. et al. Angular shaping of fluorescence from synthetic opal-based photonic crystal. Nanoscale Res Lett 10, 97 (2015). https://doi.org/10.1186/s11671-015-0781-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s11671-015-0781-y