Magic Mathematical Relationships for Nanoclusters—Errata and Addendum

Abstract

We correct magic formulas for body centered cubic (bcc) structures. The logical rational for this is further corroborated by calculations of the radial distribution function (RDF) for several crystal structures. We add results for truncated cubes which may be found in nature.

Introduction

We recently presented magic formulas for several crystal nanoclusters [1]. However, it is known to crystallographers that bcc structures have a bulk coordination of eight. The RDF determines the nearest neighbor peaks from a central point, and the integrated peak intensity reflects the corresponding coordination for those neighbors. We use an established method [2] to calculate the RDF for several crystals. Since ideal bcc cubes have coordination cn=1, we provide results for truncated bcc and face centered cubic (fcc) clusters.

Main Text

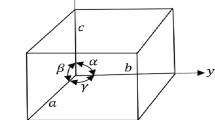
In reviewing the many magic formulas appearing in [1], it occurred to us that equation (1), which defines the adjacency matrix, depends on the crystal structure.

$$ \mathbf{A}(i,j)=\left\{\begin{array}{ll} 1& \text{if}\ r_{ij}< r_{c}\ \text{and}\ i\ne j\\ 0& \text{otherwise} \end{array}\right. $$

(1)

Here, r_ij is the Euclidean distance between atom i and atom j. While it is true that r_c=1.32·r_min is necessary for the different bond lengths in the dodecahedral structure, for the bcc structure, this is not the case. We have calculated [2] the RDF for selected structures, and some of the nearest neighbors are tabulated below (Table 1). The RDF has peak locations at neighbor sites, and the integrated intensity of the corresponding peak gives the coordination. We normalize the peaks in R(r) by dividing by the first peak, thus the peak locations become dimensionless. As the table indicates, bcc structures have $r_{c} = 2/\sqrt {3} \cdot r_{\text {min}} \approx 1.15 \cdot r_{\text {min}}$, which means the adjacency matrix must be changed, and thus the magic formulas. Note that neighbor peaks are not the same as shells, which give rise to the “magic numbers.” The dodecahedron is a complicated case, where the third neighbors appear at r₂=1.31·r_min. This case is challenging, and requires more analysis, which is in progress. The corrected bcc results are shown below (Tables 2, 3, 4, 5 and 6). These results agree with those in van Hardeveld and Hartog [3] if one shifts the index by one, i.e., we use the sequence 0, 1, 2... and they use 1, 2, 3... as their sequence. While perfect cubes may be of interest mathematically, they are not likely to appear in nature, due to single bonds at the corners. We have therefore generated truncated bcc and fcc cubes with the corners removed and their results are included in (Tables 7 and 8). The magic formulas of the indices for selected clusters are summarized in Table 9.

Table 1 Neighbor peaks in the normalized RDF for several structures

Table 2 Magic formulas for the bcc cube

Table 3 Magic formulas for the bcc octahedron

Table 4 Magic formulas for the bcc truncated octahedron

Table 5 Magic formulas for the bcc rhombic dodecahedron

Table 6 Magic formulas for the bcc cuboctahedron

Table 7 Magic formulas for the bcc truncated cube

Table 8 Magic formulas for the fcc truncated cube

Table 9 Magic topological formulas for BCC and FCC clusters

Conclusions

We have corrected magic formulas for bcc structures and added results from the RDF and for truncated bcc and fcc cubes.